Sin x 1 решить неравенство

Обновлено: 07.07.2024

Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> --> Введите тригонометрическое уравнение
Решить уравнение

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу. Т.к. желающих решить задачу очень много, ваш запрос поставлен в очередь.
Через несколько секунд решение появится ниже.
Пожалуйста подождите сек.

Неравенства вида $ tg \;x > a $ и \( tg \;x

Пусть дано простейшее неравенство $ tg \;x > a $.
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом $a \in \mathbb $ решение неравенства будет таким:
$$ x \in \left(arctg \;a + \pi k; \;\; \frac<\pi> + \pi k \right), \; k \in \mathbb $$

Пусть дано простейшее неравенство \( tg \;x

Уравнения, сводящиеся к квадратным

Решить уравнение 2 cos 2 (х) - 5 sin(х) + 1 = 0

Заменяя cos 2 (х) на 1 - sin 2 (х), получаем
2 (1 - sin 2 (х)) - 5 sin(х) + 1 = 0, или
2 sin 2 (х) + 5 sin(х) - 3 = 0.
Обозначая sin(х) = у, получаем 2у 2 + 5y - 3 = 0, откуда y₁ = -3, y₂ = 0,5
1) sin(х) = - 3 — уравнение не имеет корней, так как |-3| > 1;
2) sin(х) = 0,5; $ x = (-1)^n \text(0,5) + \pi n = (-1)^n \frac<\pi> + \pi n, \; n \in \mathbb $
Ответ $ x = (-1)^n \frac<\pi> + \pi n, \; n \in \mathbb $

Решить уравнение 2 cos 2 (6х) + 8 sin(3х) cos(3x) - 4 = 0

Используя формулы
sin 2 (6x) + cos 2 (6x) = 1, sin(6х) = 2 sin(3x) cos(3x)
преобразуем уравнение:
3 (1 - sin 2 (6х)) + 4 sin(6х) - 4 = 0 => 3 sin 2 (6х) - 4 sin(6x) + 1 = 0
Обозначим sin 6x = y, получим уравнение
3y 2 - 4y +1 =0, откуда y₁ = 1, y₂ = 1/3

1) $ sin(6x) = 1 \Rightarrow 6x = \frac<\pi> +2\pi n \Rightarrow x = \frac<\pi> +\frac<\pi n>, \; n \in \mathbb $
2) $ sin(6x) = \frac<1> \Rightarrow 6x = (-1)^n \text \frac<1> +\pi n \Rightarrow $
$ \Rightarrow x = \frac \text \frac<1> +\frac<\pi n>, \; n \in \mathbb $
Ответ $ x = \frac<\pi> +\frac<\pi n>, \;\; x = \frac \text \frac +\frac<\pi n>, \; n \in \mathbb $

Неравенства вида $ \cos x > a $ и \( \cos x

Пусть дано простейшее неравенство $ \cos x > a $.
1) При $-1 1$ решением неравенства является любое действительное число: $ x \in \mathbb $
3) При $a \leqslant -1$ неравенство не имеет решений.
4) При $a = 1$ решением неравенства является любое действительное число, отличное от $ 2\pi k, \; k \in \mathbb $

Уравнение sin(х) = а

Из определения синуса следует, что $ -1 \leqslant \sin \alpha \leqslant 1 $. Поэтому если |a| > 1, то уравнение sin x = а не имеет корней. Например, уравнение sin x = 2 не имеет корней.

Уравнение sin х = а, где $ |a| \leqslant 1 $, на отрезке $ \left[ -\frac<\pi>; \; \frac<\pi> \right] $ имеет только один корень. Если $ a \geqslant 0 $, то корень заключён в промежутке $ \left[ 0; \; \frac<\pi> \right] $; если а

Тригонометрические неравенства

Решение тригонометрических уравнений

Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.

Уравнение tg(х) = а

Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.

Уравнение tg x = а для любого a имеет на интервале $ \left( -\frac<\pi>; \; \frac<\pi> \right) $ только один корень. Если $ |a| \geqslant 0 $, то корень заключён в промежутке $ \left[ 0; \; \frac<\pi> \right) $; если а

Уравнение вида a sin(x) + b cos(x) = c

Решить уравнение 2 sin(x) + cos(x) - 2 = 0

Используя формулы $ \sin(x) = 2\sin\frac \cos\frac, \; \cos(x) = \cos^2 \frac -\sin^2 \frac $ и записывая правую часть уравпения в виде $ 2 = 2 \cdot 1 = 2 \left( \sin^2 \frac + \cos^2 \frac \right) $ получаем

$ 4\sin\frac \cos\frac + \cos^2 \frac - \sin^2 \frac = 2\sin^2 \frac + 2\cos^2 \frac $

Поделив это уравнение на $ \cos^2 \frac $ получим равносильное уравнение $ 3 \text^2\frac - 4 \text\frac +1 = 0 $
Обозначая $ \text\frac = y $ получаем уравнение 3y 2 - 4y + 1 = 0, откуда y₁=1, y₁= 1/3

1) $ \text\frac = 1 \Rightarrow \frac = \frac<\pi> +\pi n \Rightarrow x = \frac<\pi> +2\pi n, \; n \in \mathbb $
2) $ \text\frac = \frac \Rightarrow \frac = \text\frac +\pi n \Rightarrow x = 2 \text \frac +2\pi n, \; n \in \mathbb $
Ответ $ x = \frac<\pi> +2\pi n, \;\; x = 2 \text \frac +2\pi n, \; n \in \mathbb $

В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях $ a \neq 0, \; b \neq 0, \; c \neq 0, \; c^2 \leqslant b^2+c^2 $ можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на $ \sqrt $:

Введём вспомогательный аргумент $ \varphi $, такой, что Таким образом, уравнение можно записать в виде
$ \sin x \cos \varphi + \cos x \sin \varphi = \frac> $
откуда Изложенный метод преобразования уравнения вида a sin(x) + b cos(x) = c к простейшему тригонометрическому уравнению называется методом введения вспомогательного угла.

Решить уравнение 4 sin(x) + 3 cos(x) = 5

Здесь a = 4, b = 3, $ \sqrt = 5 $. Поделим обе части уравнения на 5:

$ \frac<4>\sin(x) + \frac\cos(x) = 1 $
Введём вспомогательный аргумент $ \varphi $, такой, что $ \cos \varphi = \frac<4>, \; \sin \varphi = \frac $ Исходное уравнение можно записать в виде
$ \sin x \cos \varphi + \cos x \sin \varphi = 1, \;\; \sin(x+\varphi) = 1 $
откуда

Неравенства вида $ \sin x > a $ и \( \sin x

Пусть дано простейшее неравенство $ \sin x > a $.
1) При $-1 1 $ решением неравенства является любое действительное число: $ x \in \mathbb $
3) При $а = 1 $ решением неравенства является любое действительное число, отличное от $ \frac<\pi> + 2\pi k, \; k \in \mathbb $
4) При $а \leqslant -1 $ неравенство не имеет решений.

Уравнение cos(х) = а

Из определения косинуса следует, что $ -1 \leqslant \cos \alpha \leqslant 1 $. Поэтому если |a| > 1, то уравнение cos x = a не имеет корней. Например, уравнение cos х = -1,5 не имеет корней.

Уравнение cos x = а, где $ |a| \leqslant 1 $, имеет на отрезке $ 0 \leqslant x \leqslant \pi $ только один корень. Если $ a \geqslant 0 $, то корень заключён в промежутке $ \left[ 0; \; \frac<\pi> \right] $; если a

Уравнения, решаемые разложением левой части на множители

Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.

Решить уравнение sin(2х) - sin(x) = 0
Используя формулу синуса двойного аргумента, запишем уравнепие в виде 2 sin(x) cos(x) - sin(x) = 0. Вынося общий множитель sin(x) за скобки, получаем sin(x) (2 cos x - 1) = 0

2) $ 2 \cos(x) -1 =0, \; \cos(x) = \frac12, \; x = \pm \frac<\pi> +2\pi n, \; n \in \mathbb $

Решить уравнение cos(3х) cos(x) = cos(2x)
cos(2х) = cos (3х - х) = cos(3х) cos(x) + sin(3х) sin(x), поэтому уравнение примет вид sin(x) sin(3х) = 0

Заметим, что числа $ \pi n $ содержатся среди чисел вида $ x = \frac<\pi n>, \; n \in \mathbb $
Следовательно, первая серия корней содержится во второй.

Решить уравнение 6 sin 2 (x) + 2 sin 2 (2x) = 5
Выразим sin 2 (x) через cos(2x)
Так как cos(2x) = cos 2 (x) - sin 2 (x), то
cos(2x) = 1 - sin 2 (x) - sin 2 (x), cos(2x) = 1 - 2 sin 2 (x), откуда
sin 2 (x) = 1/2 (1 - cos(2x))
Поэтому исходное уравнение можно записать так:
3(1 - cos(2x)) + 2 (1 - cos 2 (2х)) = 5
2 cos 2 (2х) + 3 cos(2х) = 0
cos(2х) (2 cos(2x) + 3) = 0

Этот математический калькулятор онлайн поможет вам решить тригонометрическое неравенство. Программа для решения тригонометрического неравенства не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Неравенства вида $ ctg \;x > a $ и \( ctg \;x

Пусть дано простейшее неравенство $ ctg \;x > a $.
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом $a \in \mathbb $ решение неравенства будет таким:
$$ x \in ( \pi k; \;\; arcctg \;a + \pi k ), \; k \in \mathbb $$

Пусть дано простейшее неравенство \( ctg \;x

Тригонометрические уравнения

Решение тригонометрических неравенств

ПРИМЕР 1. Решим неравенство $ \sin x > \frac $.
Так как $ -1 \frac $.
Так как $ -1 1 $.
Очевидно, что решение неравенства будет таким:
$$ x \in \left(\frac<\pi> + \pi k; \;\; \frac<\pi> + \pi k\right), \; k \in \mathbb $$

ПРИМЕР 6. Решим неравенство $ tg \;x \frac> $.
Очевидно, что решение неравенства будет таким:
$$ x \in \left( \pi k; \;\; \frac<\pi> + \pi k \right), \; k \in \mathbb $$

Данный калькулятор предназначен для решения тригонометрических неравенств онлайн. Тригонометрические неравенства – это неравенства, в которых переменная стоит под знаком тригонометрической функции.
К простейшим тригонометрическим неравенствам относятся следующие неравенства: sinx ▼a, cosx ▼a, tgx ▼a, ctgx ▼a. Знак ▼ означает любой знак сравнения (≤, ≥, >,

Основным способом решения любых тригонометрических неравенств является сведение их к простейшим тригонометрическим неравенствам, которые указаны выше.
Преимуществом онлайн калькулятора является то, что Вам нет необходимости знать все методы решения тригонометрических неравенств. Чтобы получить ответ, укажите исходное тригонометрическое неравенство. Основные примеры функций для данного калькулятора указаны ниже.
Для получения полного хода решения нажимаем в ответе Step-by-step.

$\left(a=\operatorname<const></p> <p> \right)$

Условные обозначения единичной окружности

Итак, перво-наперво нам потребуется следующий алгоритм.

Алгоритм решения неравенств с синусом:

Ограничение алгоритма

Частные случаи при решении неравенства с синусом

Важно отметить также следующие случаи, которые гораздо удобнее решить логически, не используя вышеуказанный алгоритм.

Частный случай 1. Решить неравенство:

Следствие: аналогично решается и неравенство

Частный случай 2. Решить неравенство:

Применяя аналогичные частному случаю 1 рассуждения, получим, что левая часть неравенства меньше $1$ для всех $x \in R$, кроме точек, являющихся решением уравнения $\sin = 1$. Решая это уравнение, будем иметь:

А, значит, в ответ мы записываем: $x \in R \backslash \left\\frac<\pi> + \pi n\right\>$.

Следствие: аналогично решается и неравенство

Примеры решения неравенств с помощью алгоритма.

Пример 1: Решить неравенство:

Таким образом, решение примет вид:

$x \in \left[\frac<\pi> + 2\pi n; \frac<5\pi> + 2 \pi n\right], \ n \in Z.$

Пример 2: Решить неравенство:

Отметим на оси синусов координату $- \frac$ и проведём прямую параллельно оси косинусов и проходящую через эту точку. Отметим точки пересечения. Они будут не закрашенными, так как неравенство строгое. Знак неравенства $<$, а, значит, закрашиваем область ниже прямой, т.е. меньший полукруг. Неравенство превращаем в равенство и решаем его:

Полагая далее $n=0$, находим первую точку пересечения: $x_=-\frac<\pi>$. Наша область идёт в отрицательном направлении от первой точки, значит $n$ полагаем равным $-1$: $x_=(-1)^\frac<\pi> + \pi \cdot (-1) = -\pi + \frac<\pi> = -\frac<5\pi>$.

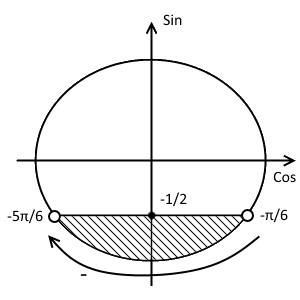
Итак, решением этого неравенства будет промежуток:

$x \in \left(-\frac<5\pi> + 2\pi n; -\frac<\pi> + 2 \pi n\right), \ n \in Z.$

Пример 3: Решить неравенство:

Этот пример решать сразу с помощью алгоритма нельзя. Для начала его надо преобразовать. Делаем в точности так, как делали бы с уравнением, но не забываем про знак. Деление или умножение на отрицательное число меняет его на противоположный!

Итак, перенесём всё, что не содержит тригонометрическую функцию в правую часть. Получим:

Разделим левую и правую часть на $-2$ (не забываем про знак!). Будем иметь:

Опять получилось неравенство, которое мы не можем решить с помощью алгоритма. Но здесь уже достаточно сделать замену переменной:

Получаем тригонометрическое неравенство, которое можно решить с помощью алгоритма:

Это неравенство было решено в примере 1, поэтому позаимствуем оттуда ответ:

$t \in \left[\frac<\pi> + 2\pi n; \frac<5\pi> + 2 \pi n\right].$

Однако, решение ещё не закончилось. Нам нужно вернуться к исходной переменной.

Представим промежуток в виде системы:

Читайте также: