Ряд маклорена для функции y sin x
Обновлено: 07.07.2024
Продолжаем рассматривать теорию и практику степенных рядов. Материал несложный, но для его понимания необходимо уже более или менее хорошо ориентировать в теме. Если Вы только-только приступили к изучению рядов или чувствуйте себя чайником, пожалуйста, начните с урока Ряды для чайников. Примеры решений. Далее следует прочитать статью Степенные ряды. Область сходимости ряда, в частности, Вы должны хорошо понимать, что такое степенной ряд и его область сходимости. А для целей сегодняшнего урока потребуется методический материал Таблица разложений некоторых функций в степенные ряды, его можно раздобыть в кладовке Математические формулы и таблицы. По возможности, таблицу лучше распечатать, поскольку она потребуется не только сейчас, но и в оффлайне.
Понятие суммы степенного ряда
Начнем подходить к теме с воспоминаний. Как мы помним, любой числовой ряд может или сходиться, или расходиться. Если числовой ряд сходится, то это значит, что сумма его членов равна некоторому конечному числу:
На уроке Степенные ряды. Область сходимости ряда мы рассматривали уже не числовые, а функциональные и степенные ряды. Возьмём тот самый подопытный степенной ряд, который всем понравился: . В ходе исследования было установлено, что этот ряд сходится при . Если числовые ряды сходятся к ЧИСЛАМ, то к чему же сходятся функциональные и степенные ряды? Правильно подумали. Функциональные ряды сходятся к ФУНКЦИЯМ. В частности, суммой ряда в его области сходимости является некоторая функция :
Еще раз подчеркиваю, что данный факт справедлив только для найденной области , вне этого промежутка степенной ряд будет расходиться.
Чтобы всё стало окончательно понятно, рассмотрим примеры с картинками. Я выпишу простейшее табличное разложение синуса в степенной ряд:
Область сходимости ряда:
(По какому принципу получены сами элементарные табличные разложения, мы рассмотрим чуть позже).
Теперь вспоминаем школьный график синуса :
Вот такая симпатичная синусоида. Хмм…. Где-то я уже это видел….
Теперь фишка. Если начертить график бесконечного многочлена , то получится… та же самая синусоида! То есть, наш степенной ряд сходится к функции . Используя признак Даламбера (см. статью Степенные ряды. Область сходимости ряда), легко проверить, что ряд сходится при любом «икс»: (собственно, поэтому в таблице разложений и появилась такая запись об области сходимости).
А что значит вообще «сходится»? По смыслу глагола – что-то куда-то идёт. Если я возьму первые три члена ряда и начерчу график многочлена пятой степени, то он лишь отдаленно будет напоминать синусоиду. А вот если составить многочлен из первых ста членов ряда: и начертить его график, то он будет с синусоидой практически совпадать (на достаточно длинном промежутке). Чем больше членов ряда – тем лучше приближение. И, как уже отмечалось, график бесконечного многочлена – есть в точности синусоида. Иными словами, ряд сходится к функции при любом значении «икс».
Рассмотрим более печальный пример, табличное разложение арктангенса:
Область сходимости ряда:
Печаль заключается в том факте, что график бесконечного многочлена существует и совпадает с графиком арктангенса только на отрезке (т.е. в области сходимости ряда):
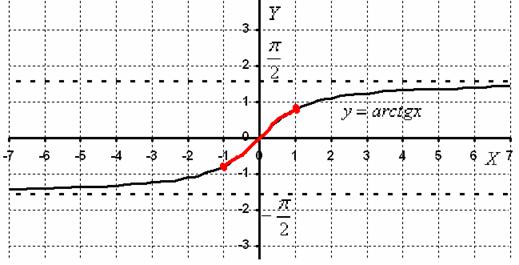
Вне отрезка разложение арктангенса в ряд расходится, и о графике речи не идёт вообще, поскольку каждое значение бесконечного многочлена бесконечно .
Исходя из вышесказанного, можно сформулировать две взаимно обратные задачи:
– найти сумму ряда (функцию) по известному разложению;
– разложить функцию в ряд (если это возможно) и найти область сходимости ряда.
Что проще? Конечно же, разложение – с него и начнём. После чего я рекомендую не затягивать и в ближайшие часы-дни (пока свежи воспоминания) потренироваться в нахождении суммы степенного ряда.
Разложение функций в степенной ряд.
Ряд Тейлора. Ряд Маклорена
Приступим к увлекательному занятию – разложению различных функций в степенные ряды. Сначала пара формул, затем практические задания.
Если функция в некотором интервале раскладывается в степенной ряд по степеням , то это разложение единственно и задается формулой:
Примечания: надстрочный индекс в последнем слагаемом обозначает производную «энного» порядка. Вместо буквы «а» в литературе часто можно встретить букву .
Данная формула носит фамилию англичанина Тейлора (ударение на первый слог).
На практике процентах в 95-ти приходится иметь дело с частным случаем формулы Тейлора, когда :
Этот ряд получил известность благодаря шотландцу Маклорену (ударение на второй слог). Разложение Маклорена также называют разложением Тейлора по степеням .
Вернемся к таблице разложений элементарных функций и выведем разложение экспоненциальной функции:
Как оно получилось? По формуле Маклорена:
Рассмотрим функцию , тогда:
Теперь начинаем находить производные в точке : первую производную, вторую производную, третью производную и т.д. Это просто, поскольку при дифференцировании экспонента превращается в саму себя:
Совершенно очевидно, что
Подставляем единицы в формулу Маклорена и получаем наше табличное разложение!
Аналогично можно вывести некоторые другие табличные разложения (но далеко не все выводятся именно так).
Примеры разложения функций в ряд Маклорена
В данном параграфе мы рассмотрим типовую задачу на разложение функции в ряд Маклорена и определении области сходимости полученного ряда. Нет, мучаться с нахождением производных не придется, мы будем пользоваться таблицей.
Разложить функцию в ряд Маклорена. Найти область сходимости полученного ряда.
! Эквивалентная формулировка: Разложить функцию в ряд по степеням
Решение незамысловато, главное, быть внимательным.
Конструируем наш ряд. Плясать начинают, как правило, от функции, разложение которой есть в таблице:
В данном случае :
Раскрываем наверху скобки:
Теперь умножаем обе части на «икс»:
В итоге искомое разложение функции в ряд:
Как определить область сходимости? Чем постоянно проводить очевидные рассуждения, проще запомнить: разложения синуса, косинуса и экспоненты сходятся при любом действительном значении (за исключением, конечно, тех случаев, когда, например, – см. комментарии к табличным разложениям). Домножение на «икс» не играет никакой роли в плане сходимости, поэтому область сходимости полученного ряда:
Разложить функцию в ряд по степеням . Найти область сходимости ряда.
Это пример для самостоятельного решения.
Я не стал рассматривать простейшие разложения вроде , или , поскольку это фактически задача в одно действие. В нужные табличные разложения вместо «альфы» необходимо подставить , , и немного причесать полученные ряды. Единственное предостережение – не теряйте по невнимательности степени и знаки.
А сейчас для разнообразия рассмотрим что-нибудь с минусами.
Разложить функцию в ряд по степеням . Найти область сходимости ряда.
В таблице находим похожее разложение:
Трюк прост – перепишем нашу функцию немного по-другому:
Таким образом, и:
Теперь нужно определить область сходимости. Согласно таблице, ряд сходится при .
В данном случае :
Так как квадрат неотрицателен, то при раскрытии модуля знак «минус» просто испаряется:
Исследуем сходимость ряда на концах найденного интервала. Значения , не входят в область определения функции , но как мы видели в Примере 2, в «проблемной» точке САМ РЯД сходиться может. И поэтому от греха подальше лучше выполнить прямую подстановку концов интервала в найденное разложение. При получаем: – расходящийся гармонический ряд. И он же получается при
Таким образом, область сходимости ряда:
Но так бывает далеко не всегда:
Простейшее разложение из учебника сходится ещё в одной точке: . Здесь значение тоже вне игры, а вот при сумма получившегося знакочередующегося ряда в точности равна .
Интересно отметить, что разложение в ряд такого логарифма:
– сходится уже на обоих концах интервала: (при подстановках , получается тот же самый сходящийся ряд )
Таким образом, с логарифмами нужно работать осмотрительно!
Пара примеров для самостоятельного решения:
Разложить функцию в ряд по степеням . Найти область сходимости ряда.
Пляска традиционно начинается от «главной» функции, то есть, начинать нужно с экспоненты.
Разложить функцию в ряд по степеням . Найти область сходимости ряда.
Здесь разложение не такое сложное, но могут возникнуть трудности с нахождением области сходимости полученного ряда.
Полные решения и ответы в конце урока.
Не редкость, когда перед разложением функции в ряд её необходимо предварительно преобразовать. Канонический случай – это разложение функции . Перед тем как ее раскладывать в ряд, необходимо понизить степень с помощью известной тригонометрической формулы: . Решать я этот пример не буду, поскольку он довольно простой, к тому же что-то подобное мы недавно рассмотрели.
Разложить функцию в ряд по степеням . Найти область сходимости ряда.
Смотрим в таблицу и находим наиболее похожее разложение:
Во-первых, вверху должна быть единица, поэтому представляем нашу функцию в виде произведения:
Теперь нам нужно в знаменателе устроить , для этого выносим двойку за скобки:
И сокращаем на два:
В данном случае , таким образом:
В итоге искомое разложение:
Определим область сходимости ряда. Можно пойти длинным и надежным путем – использовать признак Даламбера для полученного степенного ряда , т.е. найти интервал сходимости и т.д. Но можно поступить проще. В таблице указано, что биномиальный ряд сходится при . В данном случае , поэтому:
Умножаем все части неравенства на :
– интервал сходимости полученного ряда.
Что происходит с рядом на концах интервала?
При получаем: – данный ряд расходится, т.к. не выполнен необходимый признак сходимости,
и при: – расходится по той же причине.
Таким образом, область сходимости полученного ряда:
Разложить функцию в ряд по степеням . Найти область сходимости ряда.
Указание: предварительно функцию следует упростить, используя свойство логарифмов:
Это пример для самостоятельного решения.
Разложение функций в ряд Маклорена необходимо проводить и в ряде других задач, например, в задаче приближенного вычисления определенного интеграла. Кстати, там, помимо нового материала, можно посмотреть примеры других разложений, которые не поместились в этот урок.
Примеры разложения функций в ряд Тейлора по степеням , когда
Данное задание является более сложным и встречается значительно реже, но всё-таки 2-3 примера не помешают. Пригодится.
Вытащим из чулана общую формулу Тейлора:
Еще раз повторю, что вместо буквы «а» на практике часто можно встретить букву .
В чём сложность разложения функции по степеням при ненулевом значении «а»? Сложность состоит в том, что нам не удастся воспользоваться табличными разложениями, и придётся самостоятельно находить и вычислять производные. Или не придётся. Но сначала разберём универсальный «классический» метод с производными.
Очень хорошо если вы проработали урок Производные высших порядков, впрочем, я постараюсь максимально подробно закомментировать оставшиеся задачи.
И сразу небольшой Пример 8
Разложить функцию в ряд Тейлора по степеням
В данном случае , смотрим на формулу Тейлора, и становится уже всё понятнее.
Теперь предстоит ручная работа по конструированию разложения:
, все производные, начиная с четвёртой производной, будут нулевыми.
Теперь подставляем весь найденный скарб в формулу Тейлора:
Готово. Для проверки можно раскрыть скобки:
Получен исходный многочлен, что и требовалось проверить.
Рассмотрим более содержательные примеры.
Разложить функцию в ряд Тейлора по степеням . Найти область сходимости полученного ряда.
Решение: Используем разложение функции в ряд Тейлора по степеням
Хех, опять предстоит ручная работа….
В данном случае:
Замечаем, что с такими раскладами производные можно находить до бесконечности. Поэтому необходимо уловить некоторую закономерность. Найдем ещё третью производную:
А теперь проанализируем найденные производные:
Закономерность прослеживается: знаки чередуются, в числителе накручивается факториал, а в знаменателе растёт степень.
Теперь, исходя из выявленной закономерности, нужно составить производную «энного» порядка. В данном случае она выглядит так:
Как проверить, правильно ли составлена энная производная? Подставьте в неё значения , , и у вас должны получиться в точности первая, вторая и третья производные. После того, как мы убедились в том, что энная производная составлена правильно, подставляем в неё наше значение:
Теперь осталось все труды подставить в формулу Тейлора и аккуратно провести упрощения:
Далее необходимо найти область сходимости полученного степенного ряда . Это стандартная задача, которую мы многократно прорешивали на уроке Степенные ряды. Область сходимости ряда. Впрочем, из того соображения, что на концах интервала должны сократиться «двойки в степени эн», ответ нетрудно «углядеть» и устно: .
Теперь способ второй. Он основан на замене переменной. Итак, требуется разложить ту же функцию в ряд Тейлора по степеням , и мы проводим замену:
, откуда выражаем – и подставляем в нашу функцию:
при этом общая формула Тейлора превращается в формулу Маклорена:
и появляется возможность воспользоваться теми же табличными разложениями!
Таким образом, наша задача свелась к задаче предыдущего параграфа, представим полученную функцию в виде:
и воспользуемся разложением:
., в данном случае :
, после чего вспоминаем о том, что и записываем искомое разложение:
, и проверочка заодно получилась.
Возникает вопрос: а зачем тогда возиться с производными? И ответ здесь такой: замена далеко не всегда приводит к желаемому результату, так, например, она совершенно бесполезна в Примере 8, и ещё много для каких функций. Поэтому главным и основополагающим методом следует считать прямое построение ряда через производные.
Заключительный пример для самостоятельного решения:
Разложить функцию в ряд Тейлора по степеням . Найти область сходимости полученного ряда.
В образце приведены оба способа решения.
Как ваш тонус? Я так и знал, что на высоте! – поэтому самое время потренироваться в нахождении сумм степенных рядов по известным разложениям. Кроме того, на следующем уроке много интересной и. неожиданной информации. Только не злоупотребляйте =)
Решения и ответы:
Пример 2: Решение: используем разложение: .
В данном случае
Область сходимости ряда: .
! Примечание: здесь может сложиться впечатление, что из области сходимости ряда следует исключить точку , которая не входит в область определения функции, однако тут речь идёт об области сходимости ряда. А полученный ряд преспокойно сходится в точке – но не к исходной функции, а к изолированному значению: . Интересно отметить, что здесь функция терпит устранимый разрыв: и сумма степенного ряда непрерывна.
Пример 4: Решение: используем разложение: .
В данном случае
Конструируем функцию дальше:
Окончательно:
Ряд сходится при
Примечание: в точке ряд сходится не к исходной функции, а к нулю:
Пример 5: Решение: используем частный случай биномиального разложения:
В данном случае
Таким образом:
Само по себе разложение не слишком сложное, важно правильно найти область сходимости полученного ряда. Есть длинный путь и есть короткий.
Путь короткий: биномиальный ряд сходится при (см. таблицу).
В данном случае :
.
Делим все части на 3 и извлекаем из всех частей кубический корень:
– интервал сходимости ряда.
Исследуем сходимость нашего ряда на концах найдённого интервала:
и на правом конце:
Оба числовых ряда расходятся, так как не выполнен необходимый признак сходимости рядов.
Таким образом, область сходимости ряда:
Путь длинный (но более надежный и универсальный) состоит в исследовании полученного ряда с помощью признака Даламбера по стандартной схеме, рассмотренной на уроке Степенные ряды. Область сходимости ряда.
Пример 7: Решение: преобразуем функцию:
Используем разложение:
В данном случае
Таким образом:
Или в свёрнутом виде:
Найдем область сходимости полученного степенного ряда. Согласно таблице, использованное разложение сходится при . В данном случае , поэтому:
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
при – расходится;.
Таким образом, область сходимости полученного степенного ряда:
Пример 10: Решение, способ первый: Используем разложение функции в ряд Тейлора по степеням :
В данном случае:
…
…
Таким образом:
Область сходимости полученного степенного ряда уже надоела =)
Ответ:
ряд сходится при .
Способ второй: проведём замену , выразим – и подставим в функцию:
Используем разложение , в данной задаче :
обратная замена :
– искомое разложение.
Автор: Емелин Александр
(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Чтобы разложить в ряд Маклорена онлайн, то перейдите на страницу сервиса
По определению, разложить в ряд Маклорена функцию - это разложить эту соотвествующую функцию в ряд Тейлора в точке x=0.
Чтобы не быть голословным, приведём пример:
Нам необходить разложить функцию x*sin(x) в ряд Маклорена до 9-ой степени x, для это вводим в калькуляторе Ряд Тейлора данные таким образом:
Функция f(x): x*sin(x)
Разложить в ряд в точке: 0 (как раз ряд Маклорена === ряду Тейлора в точке x=0)
Введите функцию, которую будете раскладывать в ряд Тейлора
Выполним разложение функции f(x) в ряд Тейлора в точки x0 до n-го члена.
Данный калькулятор также знает как разложить функцию в степенной ряд.
Другие функции
С применением степени
(квадрат и куб) и дроби
С применением синуса и косинуса
Гиберболические синус и косинус
Гиберболические тангенс и котангенс
Гиберболические арксинус и арккосинус
Гиберболические арктангенс и арккотангенс
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке): absolute(x) Абсолютное значение x(модуль x или |x|) arccos(x) Функция - арккосинус от x arccosh(x) Арккосинус гиперболический от x arcsin(x) Арксинус от x arcsinh(x) Арксинус гиперболический от x arctg(x) Функция - арктангенс от x arctgh(x) Арктангенс гиперболический от x exp(x) Функция - экспонента от x (что и e^x) log(x) or ln(x) Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) sin(x) Функция - Синус от x cos(x) Функция - Косинус от x sinh(x) Функция - Синус гиперболический от x cosh(x) Функция - Косинус гиперболический от x sqrt(x) Функция - квадратный корень из x sqr(x) или x^2 Функция - Квадрат x ctg(x) Функция - Котангенс от x arcctg(x) Функция - Арккотангенс от x arcctgh(x) Функция - Гиперболический арккотангенс от x tg(x) Функция - Тангенс от x tgh(x) Функция - Тангенс гиперболический от x cbrt(x) Функция - кубический корень из x gamma(x) Гамма-функция LambertW(x) Функция Ламберта x! или factorial(x) Факториал от x В выражениях можно применять следующие операции: Действительные числа вводить в виде 7.5, не 7,5 2*x - умножение 3/x - деление x^3 - возведение в степень x + 7 - сложение x - 6 - вычитание 15/7 - дробь
Другие функции: asec(x) Функция - арксеканс от x acsc(x) Функция - арккосеканс от x sec(x) Функция - секанс от x csc(x) Функция - косеканс от x floor(x) Функция - округление x в меньшую сторону (пример floor(4.5)==4.0) ceiling(x) Функция - округление x в большую сторону (пример ceiling(4.5)==5.0) sign(x) Функция - Знак x erf(x) Функция ошибок (или интеграл вероятности) laplace(x) Функция Лапласа asech(x) Функция - гиперболический арксеканс от x csch(x) Функция - гиперболический косеканс от x sech(x) Функция - гиперболический секанс от x acsch(x) Функция - гиперболический арккосеканс от x
Постоянные: pi Число "Пи", которое примерно равно
3.14159.. e Число e - основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности - знак для бесконечности

,
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х , если:
1) она имеет производные всех порядков;
2) построенный ряд сходится в этой точке.
При а =0 получаем ряд, называемый рядом Маклорена:
,
Разложение простейших (элементарных) функций в ряд Маклорена:
Показательные функции
, R=∞
Тригонометрические функции
, R=∞
, R=∞
, (-π/2 < x < π/2), R=π/2
Функция actgx не разлагается по степеням x, т.к. ctg0=∞
Гиперболические функции
Логарифмические функции
, -1<x<1 , R = 1
Биномиальные ряды
.

Пример №1 . Разложить в степенной ряд функцию f(x)=2 x .
Решение. Найдем значения функции и ее производных при х=0
f(x) = 2 x , f(0) = 2 0 =1;
f'(x) = 2 x ln2, f'(0) = 2 0 ln2= ln2;
f''(x) = 2 x ln 2 2, f''(0) = 2 0 ln 2 2= ln 2 2;
…
f (n) (x) = 2 x ln n 2, f (n) (0) = 2 0 ln n 2= ln n 2.
Подставляя полученные значения производных в формулу ряда Тейлора, получим:
Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -∞<x<+∞.

Пример №2 . Написать ряд Тейлора по степеням (х+4) для функции f(x)=e x .
Решение. Находим производные функции e x и их значения в точке х=-4.
f(x) = е x , f(-4) = е -4 ;
f'(x) = е x , f'(-4) = е -4 ;
f''(x) = е x , f''(-4) = е -4 ;
…
f ( n ) (x) = е x , f ( n ) ( -4) = е -4 .
Следовательно, искомый ряд Тейлора функции имеет вид:
Данное разложение также справедливо для -∞<x<+∞.
Пример №3 . Разложить функцию f(x)=lnx в ряд по степеням (х-1),
( т.е. в ряд Тейлора в окрестности точки х=1).
Решение. Находим производные данной функции.
f(x)=lnx , , , ,
f(1)=ln1=0, f'(1)=1, f''(1)=-1, f'''(1)=1*2. f (n) =(-1) n-1 (n-1)!
Подставляя эти значения в формулу, получим искомый ряд Тейлора:
С помощью признака Даламбера можно убедиться, что ряд сходится при ½х-1½<1 . Действительно,
Ряд сходится, если ½х-1½<1, т.е. при 0<x<2. При х=2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х=0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].
Пример №4 . Разложить в степенной ряд функцию .
Решение. В разложении (1) заменяем х на -х 2 , получаем:
, -∞<x<∞
Пример №5 . Разложить в ряд Маклорена функцию .
Решение. Имеем
Пользуясь формулой (4), можем записать:
подставляя вместо х в формулу –х , получим:
Отсюда находим: ln(1+x)-ln(1-x) = -
Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим
. Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.
Замечание.
Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а) m , где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена.
Этот метод основан на теореме о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.
Пример №5а . Разложить в ряд Маклорена функцию , указать область сходимости.
Решение. Сначала найдем 1-x-6x 2 =(1-3x)(1+2x) , далее разложим дробь с помощью сервиса.
на элементарные:
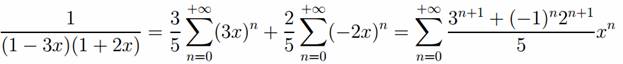
Дробь 3/(1-3x) можно рассматривать как сумму бесконечно убывающей геометрической прогрессии знаменателем 3x, если |3x| < 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
с областью сходимости |x| < 1/3.
Пример №6 . Разложить функцию в ряд Тейлора в окрестности точки х =3.
Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5):
=
Полученный ряд сходится при или –3<x-3<3 , 0< x < 6 и является искомым рядом Тейлора для данной функции.
Пример №7 . Написать ряд Тейлора по степеням ( х -1) функции ln(x+2) .
Решение.
Ряд сходится при , или -2 < x < 5.
Пример №8 . Разложить функцию f(x)=sin(πx/4) в ряд Тейлора в окрестности точки x =2.
Решение. Сделаем замену t=х-2 :
Воспользовавшись разложением (3), в котором на место х подставим π /4t, получим:
Полученный ряд сходится к заданной функции при -∞< π /4t<+∞, т.е. при (-∞<x<+∞).
Таким образом,
, (-∞<x<+∞)
Приближенные вычисления с помощью степенных рядов
- если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена.
- если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.
- в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа: a<c<x (или x<c<a).
Пример №1 . Вычислить ln(3) с точностью до 0,01.
Решение. Воспользуемся разложением , где x=1/2 (см. пример 5 в предыдущей теме):
Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:
Таким образом, мы можем отбросить этот остаток и получаем
Пример №2 . Вычислить с точностью до 0,0001.
Решение. Воспользуемся биномиальным рядом. Так как 5 3 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=5 3 +5.
так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
, поэтому его и следующие за ним члены можно отбросить.
Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подынтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.
Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:
Так как полученный ряд удовлетворяет условиям Лейбница и достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
Таким образом, находим
.
Читайте также:

