Пространство решений однородного лду 2 го порядка теорема о его размерности
Обновлено: 05.07.2024
Система линейно независимых решений уравнения (4.2) , , …, называется Фундаментальной системой решений.
Теорема 1. Любое однородное линейное Дифференциальное уравнение имеет фундаментальную систему решений.
Доказательство. Возьмем и рассмотрим различных наборов начальных условий:
Эти наборы начальных условий соответствует некоторым решениям уравнения (4.2) . Покажем, что эти решения линейно независимы. В силу начальных условий вронскиан решений имеет вид
Поскольку , то рассмотренные функции линейно независимы, поэтому образуют фундаментальную систему решений.
Примечание. Из доказательства теоремы очевидно, что для уравнения (4.2) существует бесчисленное множество фундаментальных систем решений.
Теорема 2. Любое неособенное линейное преобразование фундаментальной системы решений однородного линейного Дифференциального уравнения образует фундаментальную систему решений.
Доказательство. Пусть – фундаментальная система решений уравнения (4.2). С помощью линейного преобразования получим новую систему функций:
Здесь – некоторые числа. Пусть матрица такого преобразования
Поскольку по условию теоремы преобразование неособенное, то .
Докажем, что функции , , …, образуют фундаментальную систему решений. То, что эти функции являются решениями уравнения (4.2), вытекает из следствия основных теорем 1 и 2 для однородных линейных дифференциальных уравнений из предыдущего подраздела. Докажем, что эти решения линейно независимы. Составим вронскиан для новой системы функций
Пусть – матрица, определителем которой является данный вронскиан. Тогда
Из этого равенства следует, что
Определители в правой части этого равенства отличны от нуля, поэтому
Ни при одном значении . А это и значит, что функции линейно независимы. Следовательно, эти функции образуют фундаментальную систему решений.
Размерность пространства решений ЛОДУ n-го порядка равна n.
Док-во: нужно доказать, что существует базис пространства решений, состоящий из частных решений, т.е. частные решения , которые удовлетворяют следующим условиям:

1. Они линейно независимы на
2. Любое частное решение имеет вид
1. рассмотрим частные решения ЛОДУ , удовлетворяющие начальным условиям:

– фиксированная точка интервала .
По теореме существования и единственности решения задачи Коши определены на всем интервале .
Т.к. , то функции – линейно независимы на , т.к. иначе должен был бы равняться нулю.

2. Рассмотрим произвольное частное решение .
Оно удовлетворяет некоторым начальным условиям:


Рассмотрим частное решение . Оно удовлетворяет начальным условиям:

Т.е. и удовлетворяют одинаковым начальным условиям в точке . По теореме о единственности решения

Опр. Система n линейно независимых частных решений ЛОДУ n-го порядка называется фундаментальной системой решений (ФСР) ЛОДУ.
ФСР – базис линейного пространства решений.
Теорема о структуре общего решения ЛОДУ n-го порядка

Пусть – ФСР. Тогда общее решение имеет вид:


– произвольные постоянные.
Док-во: нужно доказать, что для такие, что частное решение удовлетворяет начальным условиям:

.
Решение , удовлетворяющее данным начальным условиям, существует и определено на всем . линейному пространству решений и разлагается по базису линейного пространства:
Используя свойства линейного дифференциального оператора, сформулируем свойство решений линейного дифференциального уравнения (4), которое дает ключ к пониманию структуры (устройства) общего решения.
Известно, что общее решение уравнения n-го порядка содержит n произвольных констант. В связи с этим возникают следующие вопросы. Можно ли найти такие n решений j1(х), j2(х), . jn(х), что функция
j (х) = , (5)
На основании свойства решений линейных однородных дифференциальных уравнений можно сделать вывод, что множество всех решений данного уравнения образует линейное пространство. Известно, что в любом линейном пространстве каждый элемент является линейной комбинацией базиса.
Введем понятия линейной зависимой и линейной независимой системы функций.
Определение 2.Система функций y1(х), y2(х), . , ym(х) называется линейно зависимой на интервале (a, b), если на этом интервале выполняется тождество:
Пример 2. Исследовать на линейную зависимость системы функций:
а) у1(х) = х, у2(х) = 3х;
б) у1(х) = sinх, у2(х) = cosх.
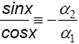
Анализируя решение примера 2, можно сформулировать утверждение общего характера: система, состоящая из двух функций, линейно зависима тогда и только тогда, когда их отношение является константой.
Для того чтобы сформулировать условия линейной зависимости системы функций, нам потребуется понятие определителя Вронского (вронскиана).
Определение 4. Определителем Вронского системы функций y1(х), y2(х), . ym(х) называется функциональный определитель порядка m:
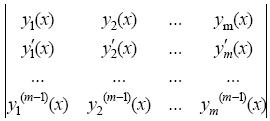
= W[y1, y2, . ym]. (7)
Пример 3. Найти определитель Вронского системы функций:
а) у1(х) = х, у2(х) = 3х;
б) у1(х) = sinх, у2(х) = cosх.
Решение. В случае (а)
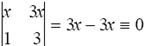
W[x, 3x] = .
Для системы функций у1(х) = sinх, у2(х) = cosх имеем
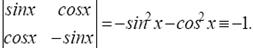
W[sinx, cosx] =
В примере 2 (а) мы установили линейную зависимость системы функций, а в примере 3 (а) показали, что ее определитель Вронского равен нулю. Данное условие является необходимым, но недостаточным. Сформулируем необходимое и достаточное условие линейной зависимости не для произвольной системы функций, а для решений линейного однородного дифференциального уравнения.

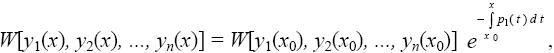
(8)
Следствие. Совокупность n решений линейного однородного дифференциального уравнения порядка n с непрерывными на (а, b) коэффициентами линейно независима тогда и только тогда, когда определитель Вронского отличен от нуля хотя бы в одной точке этого интервала.
Определение 5.Совокупность n решений линейного однородного дифференциального уравнения n-го порядка, которая определена и линейно независима на интервале (a, b), называется фундаментальной системой решений (ФСР) этого уравнения.
Теорема 4.Если коэффициенты линейного однородного дифференциального уравнения порядка n непрерывны на интервале (а, b), то для него на этом интервале существует фундаментальная система решений:
Следующая теорема дает ответ на один из основных вопросов в теории линейных дифференциальных уравнений.
pdf Лекция 1 . Первообразная и ее свойства. Неопределенный интеграл, его свойства, связь с дифференциалом. Таблица основных неопределенных интегралов.
pdf Лекция 2 . Интегрирование подстановкой и заменой переменной. Интегрирование по частям. Интегрирование выражений, содержащих квадратный трехчлен.
pdf Лекция 3 . Рациональные дроби. Разложение правильной рациональной дроби на сумму простейших (без д-ва). Интегрирование простейших дробей. Интегрирование правильных и неправильных рациональных дробей.
pdf Лекция 4 . Интегрирование выражений, рационально зависимых от тригонометрических функций. Интегрирование иррациональных функций. Примеры интегралов, не выражающихся через элементарные функции.
pdf Лекции 5-6 . Определенный интеграл как предел интегральных сумм. Теорема об интегрируемости кусочнонепрерывной функции (без д-ва). Геометрическая интерпретация определенного интеграла. Основные свойства определенного интеграла. Теоремы об оценке и о среднем значении.
pdf Лекция 7 . Определенный интеграл с переменным верхним пределом и теорема о его производной. Формула Ньютона-Лейбница. Вычисление определенных интегралов подстановкой и по частям. Интегрирование периодических функций, интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат.
Модуль 2 — «Приложения определенного интеграла»
pdf Лекция 8 . Несобственные интегралы по бесконечному промежутку (1-го рода). Несобственные интегралы от неограниченных функций на отрезке (2-го рода). Признаки сходимости несобственных интегралов. Абсолютная и условная сходимости. Несобственные интегралы с несколькими особенностями.
pdf Лекции 9-10 . Признаки сходимости несобственных интегралов. Абсолютная и условная сходимости. Несобственные интегралы с несколькими особенностями.
pdf Лекция 11 . Вычисление площадей плоских фигур, ограниченных кривыми, заданными в декартовых координатах, параметрическии и в полярных координатах.
pdf Лекции 12-13 . Вычисление объемов тел по площадям поперечных сечений и объемов тел вращения. Вычисление длины дуги и площади поверхности вращения. Метод Симпсона приближенного вычисления определенного интеграла.
Модуль 3 — «ОДУ первого порядка»
pdf Лекция 14 . Задачи, приводящие к дифференциальным уравнениям. Дифференциальное уравнение первого порядка, его решения. Частные и общие решения. Интегральные кривые. Понятие частной производной функции нескольких переменных. Задача Коши для дифференциального уравнения первого порядка. Теорема Коши о существовании решения дифференциального уравнения.
pdf Лекция 15 . Решение дифференциальных уравнений первого порядка: с разделяющимися переменными, однородных, линейных, Бернулли.
pdf Лекция 16 . Геометрическая интерпретация дифференциального уравнения первого порядка. Изоклины. Геометрическое решение дифференциальных уравнений с помощью изоклин. Особые точки и особые решения дифференциального уравнения первого порядка.
pdf Лекция 17 . Дифференциальные уравнения n-го порядка. Частные и общие решения. Задача Коши и ее геометрическая интерпретация (n=2). Теорема Коши о существовании и единственности решения дифференциального уравнения (без док-ва). Краевая задача. Понижение порядка некоторых типов дифференциальных уравнений n-го порядка.
Модуль 4 — «ОДУ высших порядков»
pdf Лекции 20-21 . Линейные однородные уравнения с постоянными коэффициентами. Характеристическое уравнение линейного однородного дифференциального уравнения. Построение общего решения по корням характеристического уравнения (вывод для n=2). Линейные неоднородные дифференциальные уравнения. Структура общего решения линейного неоднородного дифференциального уравнения. Теорема о наложении частных решений. Метод Лагранжа вариации постоянных (вывод для n=2). Структура частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами и правой частью специального вида.
pdf Лекция 22 . Нормальные системы дифференциальных уравнений. Автономные системы дифференциальных уравнений. Фазовое пространство и фазовые траектории. Задача и теорема Коши. Частные и общее решения. Сведение дифференциального уравнения высшего порядка к нормальной системе дифференциальных уравнений первого порядка. Сведение нормальной системы к дифференциальному уравнению высшего порядка (вывод для n=2). Первые интегралы системы. Понижение порядка системы дифференциальных уравнений при помощи первых интегралов. Интегрируемые комбинации. Симметрическая форма записи нормальной автономной системы дифференциальных уравнений.
pdf Лекция 23 . Системы линейных дифференциальных уравнений первого порядка. Определитель Вронского. Фундаментальная система решений. Формула Остроградского-Лиувилля. Теоремы о структуре общего решения однородной и неоднородной систем линейных дифференциальных уравнений. Метод вариации произвольных постоянных.
pdf Лекция 24 . Однородные системы линейных дифференциальных уравнений с постоянными коэффициентами. Характеристическое уравнение системы. Построение общего решения по корням характеристического уравнения (вывод только для случая действительных и различных корней).
Читайте также:

