Для вычисления значения функции y sin

Обновлено: 05.07.2024

Внимательно прочитал очень хорошие статьи от ArtemKaravaev по сложению чисел с плавающей точкой. Тема очень интересная и хочется её продолжить и показать на примерах, как работать с числами с плавающей точкой на практике. В качестве эталона возьмём библиотеку GNU glibc (libm). А чтобы статья не была уж скучной, добавим соревновательную составляющую: попробуем не только повторить, но и улучшить код библиотеки, сделав его более быстрым/точным.

В качестве примера я выбрал тригонометрическую функцию синуса. Это широко распространённая функция, математика которой хорошо известна со школы и университета. В тоже время при её имплементации появятся много ярких примеров «правильной» работы с числами. В качестве числа с плавающей точкой я буду использовать double.

В данном цикле статей планируется много всего начиная от математики, заканчивая машинными кодами и опциями компилятора. Язык написания статьи С++, но без «излишеств». В отличии от языка С, работающие примеры будут более удобочитаемыми даже для людей не знакомых с этим языком и занимать меньше строк.

Статьи будут написаны методом погружения. Будут обсуждаться подзадачи, которые потом соберутся вместе в единое решение проблемы.

Простейшее решение

Руки уже чешутся, пишем:

Как ускорить программу я думаю, что многие сообразили сразу. Как вы думаете, во сколько раз ваши изменения могут ускорить программу? Оптимизированная версия и ответ на вопрос под спойлером.

Улучшение точности

Методика

Точность вычисления функции будем определять 2-мя стандартными параметрами.

Среднеквадратичное отклонение от истинного значения sin(float128) и среднее данного отклонения. Последний параметр может дать важную информацию о том, как ведёт себя наша функция. Она может систематически занижать или завышать результат.

В дополнение к данным параметрам ввёдём еще два. Вместе с нашей функции мы вызываем ещё встроенную в библиотеку функцию sin(double). Если результаты двух функций: нашей и встроенной не совпадают (побитово), то добавляем в статистику, какая из двух функций дальше от истинного значения.

Порядок суммирования

Вернёмся снова к исходному примеру. Как можно увеличить его точность «по-быстренькому»? Те, кто внимательно читал статью Можно ли сложить N чисел типа double наиболее точно? скорее всего дадут ответ сразу. Надо крутить цикл в обратную сторону. Чтобы складывать от наименьших по-модулю, к наибольшим.

Результаты приведены в табличке.

Функция	Среднее ошибки	STD	Лучше наша	Лучше libm
sin_e1	-1.28562e-18	8.25717e-17	0.0588438%	53.5466%
sin_e3	-3.4074e-21	3.39727e-17	0.0423%	10.8049%
sin_e4	8.79046e-18	4.77326e-17	0.0686%	27.6594%
sin_e5	8.78307e-18	3.69995e-17	0.0477062%	13.5105%

Может показаться, что использование алгоритмов «умного» суммирования уберёт ошибку практически до 0, но это не так. Конечно эти алгоритмы дадут увеличение точности, но для полного избавления от ошибок требуются ещё и алгоритмы умного умножения. Они существуют, но очень накладны: очень много лишних операций. Применение их здесь не оправдано. Впрочем позднее мы к ним вернёмся в другом контексте.

Осталось совсем немного. Объединить быстрый и точный алгоритмы. Для этого снова вернёмся к ряду Тейлора. Ограничим его для примера 4-мя членами и сделаем следующее преобразование.

Можно раскрыть скобки и проверить, что получится исходное выражение. Такое представление очень просто ложится на цикл.

Работает быстро, но потеряли точность, по сравнению с e3. Опять же проблема в округлении. Давайте рассмотрим последний шаг цикла и немного преобразуем исходное выражение

И соответствующий код.

Точность в сравнении с libm увеличилась в 2 раза. Если догадываетесь почему точность увеличилась, пишите в комментариях. К тому же есть ещё одна, гораздо более неприятная вещь у sin_e4, которая отсутствует у sin_e5, связанная с точностью. Попробуйте догадаться в чём проблема. В следующей части я обязательно о ней расскажу подробно.

Если статья Вам понравится, то в следующей я расскажу, как в GNU libc считается синус с максимальным ULP в 0.548.

Написать программу вычисления значений функции y = sin(x), с помощью разложения функции в степенной ряд . Сравнить полученные значения с точными (вычисленными с помощью библиотечной функции). Вычисление синуса по формуле оформить в виде функции с двумя параметрами: значением X и значением относительной погрешности . Значение X вводятся с клавиатуры.

Решил следующим образом:

Вопрос такой) В задании требуется учесть относительную погрешность, а я решил с абсолютной. не подскажите как должно быть? Знаю только что относительная погрешность, это отношение приближенного числа к модулю абсолютной, вроде так. но как в программе реализовать, не могу понять.

Программа для вычисления значений функции заданной рядом
Написать программу для вычисления значения функции, заданной с помощью ряда. Вычисление ряда.

PS: на функцию не обращайте внимания, можно ее и проще сделать, без факториала думаю, забыл уже все. Но суть в том что бы передавать в функцию значение X и собственно нужную точность. А потом просто сравнить свою функцию с библиотечной ( из cmath ).

Добавлено через 16 минут
Вот так думаю лучше будет.

вычисления значения функции y=sin(n*x)-cos(n/x)
Помогите нужно срочно очень=), Задание:составить программу вычисления значения функции.

Вычисление значений функции y = sin(x)/(x-5)
Используя, оператор цикла While написать программу для вычисления значений функции Y = Sinx/(x-5).

Программа для вычисления значения выражения. sin(num1)+nem2.
Помогите написать программу для решения следующей задачи: На входе два вещественных числа num1 и.

Как построить таблицу значений для функции f(x)=sin(1/x)
Здравствуйте. Помогите пожалуйста. Нужно выполнить при помощи двух операторов цикла while, do while.

Найти значение функции Z = 1/4-1/4 sin ( 5/2П-8а ).Значение аргумента пользователь вводит с клавиатуры
using System; namespace ConsoleApp11 < class Program < static void.

Цикл: Вычислить sin x + sin x в квадрате + . sin x в степени n.
Даны действительное х и натуральное n. Вычислить: sin x + sin x в квадрате + . sin x в степени n.

Найти наименьшее значение функции y= sin(x) / (1+x)
Найти наименьшее значение функции y= sin(x) / (1+x) и значение аргумента, при котором оно получено.

Постановка задачи. Вычислить значение тригонометрической функции sin(x) от произвольного значения аргумента x.

Вариант решения 1. Поищем готовый вариант решения. Тригонометрия – раздел математики. Предположим, что в библиотеке System реализован класс, связанный с математическими функциями (в библиотеках прежних языков всегда была функция извлечения квадратного корня из числа – sqrt()). Как же узнать название класса?

Воспользуемся интеллектуальной подсказкой. Внутри метода Main() консольного приложения наберем одну букву M в английской раскладке. В выпадающем меню выберем класс Math (по-английски математика – Mathematics или maths). Наведя мышкой на это слово, прочитаем:
«class System.Math. Предоставляет константы и статические методы для тригонометрических, логарифмических и иных общих математических функций».
Мы почти у цели.

Программа, реализующая вычисление sin(a), угол а задан в градусах, представлена ниже:

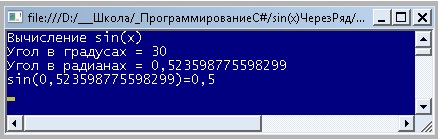
Результат выполнения программы:

Вариант решения 2.

Заглянем в справочник по высшей математике, раздел «Ряды». Из него мы узнаем, что функция sin(x) может быть представлена бесконечным рядом:

В теории, вы скажете все красиво, но бесконечный ряд – это бесконечное время вычислений, кроме того, возможно переполнение при возведении в степень и вычислении знаменателя.

То есть каждый следующий член ряда будет вносить в сумму все меньший и меньший вклад, поэтому можно использовать столько членов ряда, сколько нужно для достижения заданной точности вычислений. Например, если n=9, то | r₁₁ / r₉ | <=1/110 (более чем в 100 раз).

Что следует предпринять, если |x| >> 1 (много больше 1), ведь в этом случае наш критерий работать не будет? Тут пригодится знание такого свойства функции sin(x) как периодичность. Для угла x, заданного в радианах:
sin(x+2πk) = sin(x), где k – любое целое число, 0, ±1, ±2, ±3, … .
Для угла а, заданного в градусах:
sin(a+360°·k) = sin(a), где k – любое целое число.
Таким образом, если угол х по модулю не будет больше 2π, |x|<=2π, то тогда оценка отношения двух соседних членов ряда не превысит:
|r_n₊₂ / r_n | = 4π 2 / ((n+2)(n+1))
т.е., начиная с n=7 убывание гарантировано.

Наша функция, также как и библиотечная, получает на вход значение угла в радианах и возвращает значение sin(x). Тип аргумента и самой функции задан как double. Приступим к разработке начинки метода Sin2() – блока в фигурных скобках.

Разложение синуса в ряд Тейлора.

Функция синуса раскладывается в бесконечный ряд Тейлора.

Понятно, что бесконечный ряд мы посчитать не можем, кроме случаев, когда есть аналитическая формула бесконечной суммы. Но это не наш случай))) Предположим, что мы хотим посчитать синус в интервале . Более подробно работу с интервалами обсудим в части 3. Зная, что оценим найдём первый член который можно отбросить исходя из условия, что , где это разница между числом 1 и наименьшем числом, которое больше 1. Грубо говоря это последний бит мантиссы (wiki). Решить данное уравнение проще перебором. Для . У меня получилось уже можно отбросить. Правильный выбор количества слагаемых будет обсужден в одной из следующей частей, поэтому на сегодня «перестрахуемся» и возьмём слагаемые до включительно.
Последнее слагаемое приблизительно в 10000 раз меньше, чем .

Читайте также: