Прохождение частицы через потенциальный барьер
Обновлено: 14.05.2024
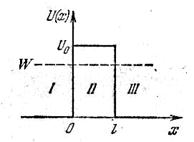
Пусть частица, движущаяся слева направо, встречает на своем пути потенциальный барьер высоты и ширины (рис. 26.1). По классическим представлениям поведение частицы имеет следующий характер. Если энергия частицы больше высоты барьера , частица беспрепятственно проходит над барьером (на участке лишь уменьшается скорость частицы, но затем при снова принимает первоначальное значение) Если же Е меньше (как изображено на рисунке), то частица отражается от барьера и летит в обратную сторону; сквозь барьер частица проникнуть не может.
Совершенно иначе выглядит поведение частицы согласно квантовой механике. Во-первых, даже при имеется отличная от нуля вероятность того, что частица отразится от барьера и полетит в обратную сторону. Во-вторых, при Е имеется отличная от нуля вероятность того, что частица проникнет «сквозь» барьер и окажется в области, где Такое, совершенно невозможное с классической точки зрения, поведение микрочастицы вытекает непосредственно из уравнения Шредингера.
Рассмотрим случай . В этом случае уравнение (21.5) имеет вид
для областей I и III и
для области II, причем
Будем искать решение уравнения (26.1) в виде (см. § 52 1-го тома). Подстановка этой функции в (26.1) приводит к характеристическому уравнению:
Таким образом, общее решение уравнения (26.1) имеет вид
Решив подстановкой уравнение (26.2), получим общее решение этого уравнения в виде
Заметим, что решение тзида соответствует волне, распространяющейся в положительном направлении оси а решение вида — волне, распространяющейся в противоположном направлении. Чтобы это понять, вспомним, что обычная (звуковая, электромагнитная и т. п.) плоская волна, распространяющаяся в направлении возрастания описывается вещественной частью выражения а волна, распространяющаяся в направлении убывания — вещественной частью выражения Частице, движущейся в положительном направлении оси сопоставляется функция (см. формулу (21.6)). Если отбросить в этой функции временной множитель, то для получится выражение Для частицы, движущейся в противоположном направлении, получится
В области III имеется только волна, прошедшая через барьер и распространяющаяся слева направо. Поэтому коэффициент в выражении (26.4) для следует положить равным нулю. Для нахождения остальных коэффициентов воспользуемся условиями, которым должна удовлетворять функция Для того чтобы была непрерывна во всей области изменений х от до должны выполняться условия: Для того чтобы была гладкой, т. е. не имела изломов, должны выполняться условия: Из этих условий вытекают соотношения:
Разделим все уравнения на и введем обозначения:
Тогда уравнения (26.7) примут вид
Отношение квадратов модулей амплитуд отраженной и падающей волны
определяет вероятность отражения частицы от потенциального барьера и может быть названо коэффициентом отражения.
Отношение квадратов модулей амплитуд прошедшей и падающей волны
определяет вероятность прохождения частицы через барьер и может быть названо коэффициентом прохождения (или коэффициентом прозрачности).
Нас будет интересовать только прохождение частиц через барьер, и мы ограничимся нахождением величины D. Правда, найдя D, легко найти R, поскольку эти коэффициенты связаны очевидным соотношением:
Умножим первое из уравнений (26.9) на i и сложим с третьим. В результате получим:
Теперь умножим второе из уравнений (26.9) на i и вычтем его из четвертого. Получим:
Решив совместно уравнения (26.11) и (26.12), найдем, что
Наконец, подставив найденные нами значения во второе из уравнений (26.9), получим выражение для :
обычно бывает много больше единицы. Поэтому в знаменателе выражения для слагаемым, содержащим множитель можно пренебречь по сравнению со слагаемым, содержащим множитель (комплексные числа и имеют одинаковый модуль). Итак, можно положить
Согласно (26.10) квадрат модуля этой величины дает вероятность прохождения частицы через потенциальный барьер. Учтя, что получим:
Выражение имеет величину порядка единицы. Поэтому можно считать, что
Из полученного нами выражения следует, что вероятность прохождения частицы через потенциальный барьер сильно зависит от ширины барьера l и от его превышения над Е, т. е. от . Если при какой-то ширине барьера коэффициент прохождения D равен, допустим, 0,01, то при увеличении ширины в два раза D станет равным , т. е. уменьшается в 100 раз. Тот же эффект в этом случае вызвало бы возрастание в четыре раза величины . Коэффициент прохождения резко уменьшается при увеличении массы частицы .
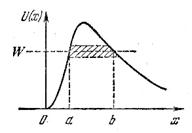
Соответствующий расчет дает, что в случае потенциального барьера произвольной фермы (рис. 26.2) формула (26,13) должна быть заменена более общей формулой:
При преодолении потенциального барьера частица как бы проходит через «туннель» в этом барьере (см. заштрихованную область на рис. 26.2), в связи с чем рассмотренное нами явление называют туннельным эффектом.
С классической точки зрения туннельный эффект представляется абсурдным, так как частица, «находящаяся в туннеле», должна была бы обладать отрицательной кинетической энергией (в туннеле ). Однако туннельный эффект — явление специфически квантовое, не имеющее аналога в классической физике. В квантовой же механике деление полной энергии на кинетическую и потенциальную не имеет смысла, так как противоречит принципу неопределенности. Действительно, тот факт, что частица обладает определенной кинетической энергией Т, был бы равнозначен тому, что частица имеет определенный импульс . Аналогично тот факт, что частица имеет определенную потенциальную энергию 0, означал бы, что частица находится в точно заданном месте пространства. Поскольку координата и импульс частицы не могут одновременно иметь определенных значений, не могут быть одновременно точно определены Т и U. Таким образом, хотя полная энергия частицы Е имеет вполне определенное значение, она не может быть представлена в виде суммы точно определенных энергий Т и V. Ясно, что в этом случае заключение об отрицательности Т «внутри» туннеля становится беспочвенным.
Рассмотрим простейший потенциальный барьер прямоугольной формы (рис. 5.4) для одномерного (по оси х) движения частицы.

Для потенциального барьера прямоугольной формы высоты U и ширины l можно записать:

При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером при E > U, либо отразится от него (E < U) и будет двигаться в обратную сторону, т.е. она не может проникнуть через барьер.
Для микрочастиц же, даже при E < U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E > U имеется также отличная от нуля вероятность, что частица окажется в области x > l, т.е. проникнет сквозь барьер. Такой вывод следует непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при данных условиях задачи.
Уравнение Шредингера для состояний каждой из выделенных областей имеет вид:
Общее решение этих дифференциальных уравнений:
В данном случае, согласно (5.4.2), – мнимое число, где
Можно показать, что A1 = 1, B3 = 0, тогда, учитывая значение q,получим решение уравнения Шредингера для трех областей в следующем виде:
В области 2 функция (5.4.4) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени не мнимые, а действительные.
Таким образом, квантовая механика приводит к принципиально новому квантовому явлению – туннельному эффекту, в результате которого микрообъект может пройти через барьер.

Коэффициент прозрачности для барьера прямоугольной формы .

Для барьера произвольной формы .
С классической точки зрения прохождение частицы сквозь потенциальный барьер при E < U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является специфическим квантовым эффектом.
Строгое квантово-механическое решение задачи о гармоническом осцилляторе приводит еще к одному существенному отличию от классического рассмотрения. Оказывается, что можно обнаружить частицу за пределами дозволенной области ( , ) (рис. 5.5), т.е. за точками 0 и l(рис. 5.1).

Это означает, что частица может прибывать там, где ее полная энергия меньше потенциальной энергии. Это оказывается возможным вследствие туннельного эффекта.
Рассматривая задачу о частице в потенциальной яме, мы считали, что на границах ямы волновая функция становится равной нулю и вероятность обнаружить частицу за пределами ямы также равна нулю. В действительности имеется определенная вероятность обнаружить электрон за пределами потенциальной ямы. Этот результат существенно отличается от выводов классической физики. Частица, подчиняющаяся законам классической физики, может выйти из потенциальной ямы только при условии, что ее полная энергия превышает «глубину» потенциальной ямы. Стенки потенциальной ямы представляют для частицы потенциальный барьер, который она не может преодолеть. Для того чтобы частица могла выйти из потенциальной ямы или проникнуть в нее, согласно классической физике, ей нужно сообщить энергию, большую высоты потенциального барьера.
Квантовая механика приводит к принципиально новому выводу о возможности прохождения частиц сквозь потенциальные барьеры.
Пусть частица, движущаяся по оси x, встречает на своем пути простейший потенциальный барьер прямоугольной формы высотой U0 и шириной l (см.рис.1).

По классическим законам, если кинетическая энергия частицы больше высоты барьера E > U0 , т. е. потенциальной энергии в области II , то частица беспрепятственно проходит эту область. Если E < U0, то частица отражается от барьера и летит в обратную сторону.
Поведение микрочастицы можно определить, решая уравнение Шредингера. Физический интерес представляет случай, когда полная энергия частицы меньше высоты потенциального барьера E < U0, поскольку в этом случае классическая физика не разрешает проникнуть частице сквозь барьер.
Для областей I и III
Решение уравнения Шредингера имеет вид
в области III , где .
в области II , где
Решение вида соответствует волне, распространяющейся в положительном направлении оси x, а решение вида - волне, распространяющейся в противоположном направлении. Решение вида соответствует возрастающей экспоненте, - убывающей. Характер поведения функций проиллюстрируем рисунком (рис.2). Видно, волновая функция не равна нулю и внутри барьера, а в области III , если барьер не слишком широк, будет опять иметь вид волн де Бройля с той же длиной волны , но с меньшей амплитудой.
Для того, чтобы функция была гладкой
Из этих условий вытекают соотношения
В области III волна, прошедшая через барьер, распространяется только в положительном направлении, поэтому коэффициент В3 = 0.
Систему из 4-х уравнений с 5-ю неизвестными решим, если сведем количество неизвестных к 4
Отношение квадратов модулей амплитуд отраженной и падающей волны
определяет вероятность отражения частицы от потенциального барьера и носит название коэффициента отражения.
Отношение квадратов модулей амплитуд прошедшей и падающей волны
определяет вероятность прохождения частицы через потенциальный барьер и может быть названо коэффициентом прохождения или коэффициентом прозрачности. Он определяет отношение плотности потока прошедших частиц к плотности потока частиц падающих.
Коэффициенты связаны между собой соотношением R + D = 1.
Дальнейшие расчеты приведут нас к следующему выражению для коэффициента прозрачности
Из полученного выражения следует, что вероятность прохождения частицы через потенциальный барьер зависит от ширины барьера и массы частицы. С увеличением массы частицы вероятность прохождения уменьшается. На вероятность прохождения также влияет превышение потенциального барьера над энергией частицы, т.е. U0 – E.
В случае потенциального барьера произвольной формы
Туннельный эффект.
При преодолении потенциального барьера частица как бы проходит через «туннель» в этом барьере, в связи с чем это явление и получило название туннельного эффекта( рис.3).

С классической точки зрения частица, «находящаяся в туннеле», должна обладать отрицательной кинетической энергией (E < U).

Однако туннельный эффект явление специфически квантовое, не имеющее аналога в классической физике. В квантовой механике деление энергии на кинетическую и потенциальную не имеет смысла, так как противоречит соотношению неопределенности.
Прохождение частиц сквозь потенциальный барьер нашло экспериментальное подтверждение в явлении автоэлектронной эмиссии электронов из металла. Вырывание электронов происходит при напряженностях электрического поля, в сотни раз меньших, чем те которые необходимы для того, чтобы электрон преодолел поверхностную разность потенциалов на границе металл-вакуум и покинул металл. Туннельный эффект играет основную роль в явлениях радиоактивного альфа-распада.
Туннельный эффект уже давно весьма эффективно используется в науке и технике. На нем основан принцип действия многих полупроводниковых приборов (туннельные диоды). Он используется в сверхчувствительных записывающих головках магнитных дисков, сканирующих туннельных микроскопах (1981). В настоящее время пространственная разрешающая способность таких микроскопов
20 нм. Для сравнения, современный оптический микроскоп, конструкция которого была изобретена в 1873 г., имеет разрешающую способность

Рассмотрим простейший потенциальный барьер прямоугольной формы для одномерного (по оси х) движения частицы. Для потенциального барьера прямоугольной формы высоты U и ширины l можем записать
При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е>U), либо отразится от него (при Е<U) и будет двигаться в обратную сторону, т. е. она не может проникнуть сквозь барьер. Для микрочастицы же, даже при Е>U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E<U имеется также отличная от нуля вероятность, что частица окажется в области х>1, т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при условиях данной задачи. С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е<U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией.

Совершенно иначе выглядит поведение частицы согласно квантовой механике. В квантовой механике с помощью уравнения Шредингера определяется коэффициент прозрачности потенциального барьера D, который равен отношению интенсивности волны, прошедшей потенциальный барьер, к интенсивности волны, падающей на барьер. Для рассматриваемой задачи находят следующее выражение:
0,36. Если же m= me, U0– W=10 эВ, l=10 -2 м, В первом случае вероятность проникновения частицы через барьер большая, во втором – ничтожно мала.
Соответствующий расчет дает, что в случае потенциального барьера произвольной формы (рис. 10.2) формула (10.1) должна быть заменена более общей формулой:
При преодолении потенциального барьера частица как бы проходит через «туннель» в этом барьере, в связи с чем рассмотренное нами явление называют туннельным эффектом.
С классической точки зрения туннельный эффект представляется абсурдным, так как частица, находящаяся в туннеле, должна обладать отрицательной кинетической энергией. Однако туннельный эффект – явление квантовое, не имеющее аналога в классической физике. В квантовой механике деление полной энергии на кинетическую и потенциальную не имеет смысла, так как противоречит принципу неопределенности. Действительно, тот факт, что частица обладает определенной кинетической энергией, был бы равнозначен тому, что частица имеет определенный импульс. Аналогично, тот факт, что частица имеет определенную потенциальную энергию U, означал бы, что частица находится в точно заданном месте пространства. А координата и импульс не могут одновременно иметь определенных значений. Таким образом, хотя полная энергия частицы Wимеет вполне определенные значения, она не может быть представлена в виде суммы точно определенных энергий Wки U. Ясно, что в этом случае заключение об отрицательности кинетической энергии внутри туннеля становится беспочвенным.
Читайте также:

