Решить уравнение sin z 2
Обновлено: 04.07.2024
Нужно воспользоваться определениями функций комплексного аргумента: $%\cos z=\frac+e^>2$% и $%\sin z=\frac-e^>$%. Удобно положить $%w=e^$%. Тогда уравнение (с учётом домножения на 2) принимает вид $%w+w^-iw+iw^=4$%. Домножая на $%w$%, приходим к квадратному уравнению $%(1-i)w^2-4w+1+i=0$%. Удобно сделать старший коэффициент равным единице, умножив на $%\frac1=\frac2$%, и тогда получится $%w^2-2(1+i)w+i=0$%.
Квадратные уравнения с комплексными коэффициентами решаются по тем же формулам, что и в действительном случае. Здесь приведённый дискриминант равен $%D/4=(1+i)^2-i=i$%, и из него надо извлечь квадратный корень. Можно заметить, что $%(1+i)^2=2i$% (это только что использовалось), откуда понятно, что $%\sqrt=\frac$%.
В итоге у нас получится $%w=1+i\pm\frac=\frac(\sqrt2\pm1)$%. Вспомним, что $%w=e^=e^=e^=e^(\cos x+i\sin x)$%. Это тригонометрическая форма комплексного числа. У нас при решении квадратного уравнения получилось $%x=(\sqrt2\pm1)(\cos\frac<\pi>4+i\sin\frac<\pi>4)$%. Теперь можно приравнять модули: $%e^=\sqrt2\pm1$%, откуда $%y=\pm\ln(\sqrt2+1)$% с учётом того, что числа $%\sqrt2\pm1$% взаимно обратны. Также приравниваем аргументы с точностью до целочисленного кратного $%2\pi$%. Это даёт $%x=\frac<\pi>4+2\pi k$%, то есть решения уравнения имеют вид $%z=\frac<\pi>4+2\pi k\pm i\ln(\sqrt2+1)$%.
отвечен 26 Янв '16 3:18
подскажите пожалуйста, а вот тут какой ответ? sin(z)-cos(z)=3. у меня что-то получается z=-(пи)/4+2(пи)к-iln(-3+(7)^(1/2))/(2^(1/2)) это верно?
Здравствуйте
There are a number of solutions to this problem online that use identities I have not been taught. Here is where I am in relation to my own coursework:
$ \exp(iz) - \exp(-iz) = 4i $
$ \exp(2iz) - 1 = 4i \cdot \exp (iz) $
Then, setting $w = \exp(iz),$ I get:
I can then use the quadratic equation to find:
$ w = i(2 \pm \sqrt 3 )$
$\exp(iz) = w = i(2 \pm \sqrt 3 ) $ implies
$ e^\cos(x) = 0 $, thus $ x = \frac<\pi> $ $ ie^\sin(x) = i(2 \pm \sqrt 3 ) $ so $ y = -\ln( 2 \pm \sqrt 3 ) $
So I have come up with $ z = \frac<\pi> - i \ln( 2 \pm \sqrt 3 )$
But the back of the book has $ z = \frac<\pi> \pm i \ln( 2 + \sqrt 3 ) +2n\pi$
Now, the $+2n\pi$ I understand because sin is periodic, but how did the plus/minus come out of the natural log? There is no identity for $\ln(a+b)$ that I am aware of. I believe I screwed up something in the calculations, but for the life of me cannot figure out what. If someone could point me in the right direction, I would appreciate it.
123 1 1 gold badge 1 1 silver badge 5 5 bronze badges $\begingroup$ Why does $e^<-y>\cos x=0$ implies $x=<\pi\over2>+2\pi k$ and not $x=<\pi\over 2>+\pi k$? @Tom $\endgroup$3 Answers 3
Your answer is actually identical to the book's solution (after accounting for $2n\pi$).
The key identity: $$ \frac> = 2 - \sqrt.$$
$\begingroup$ So, $ (2 - \sqrt3) = (2+\sqrt3)^ <-1>$ and this allows me to say for that second case $ \ln(2-\sqrt3) = -\ln(2+\sqrt3) $. Then I can combine these two cases for the imaginary part as $ \pm i\ln(2+\sqrt3) $ , correct? $\endgroup$ $\begingroup$ @am@Why : It is indeed an identity. Your argument showing how to prove it by rationalizing the denominator demonstrates that it is an identity. What does the word "identity" mean to you if this is not an identity. $\endgroup$ $\begingroup$ @abel : How you get it is shown by two methods above, in the comments. As I have understood it, an equality says two things are equal, and equation (with some conventional exceptions) is an equality whose truth is contingent on the values of some expressions involved that could be assigned different values, and an identity is an equality that is true regardless of any such values. Thus, for example, "$1+1=2$" and $e^Setting $w=e^,$ we need to solve the equation $w^2-4iw-1=0.$ The solutions to this quadratic equation are $w=i(2+\sqrt 3)$ and $w=i(2-\sqrt 3).$
Let's deal with the first solution. We need to find $z=x+iy$ such that $e^= e^e^= i(2+\sqrt 3).$ This implies $\cos x =0.$ As you point out, that has solution set $\pi/2 + n\pi, n\in \mathbb Z.$ But there is another implication: In order to get $2+\sqrt 3$ as the imaginary part, we have to delete all $\pi/2 + n\pi$ for $n$ odd, as they lead to negative imaginary values. This is why we end up with $\pi/2 + 2n\pi.$
At this point, let's say goodbye to the original post for inspiration, as things are a little cloudy there. The easiest way to do this is write $e^e^=i(2+\sqrt 3)= e^
Solving for $z$ in the case $w=i(2-\sqrt 3)$ is the same. So in all, the solutions to the original problem are $z = (\pi/2 +2n\pi) -i\ln(2\pm\sqrt 3),n\in \mathbb Z.$

Recall that the addition formula for cosines reads $$\cos(z+z')=\cos z\cos z'-\sin z\sin z',$$ and that, for $z'=-\pi/4$, one gets $$\cos(z-\pi/4)=(\cos z+\sin z)/\sqrt2.$$ Hence the equation to be solved is $$\cos(z-\pi/4)=\sqrt2.$$ To go further, consider $$u=\mathrm e^<\mathrm i(z-\pi/4)>,$$ then $u\ne0$ and the equation above reads $$u+u^=2\sqrt2,$$ that is, $$u^2-2\sqrt2u+1=0=(u-\sqrt2)^2-1,$$ that is, $$u=\sqrt2\pm1.$$ Thus, the complex number $$\mathrm i(z-\pi/4)-\log(\sqrt2\pm1)$$ must be a multiple of $2\mathrm i\pi$, that is, finally, and since $\sqrt2\pm1$ are respective inverses, $$z=\pm\mathrm i\log(\sqrt2+1)+\pi/4+2n\pi,\qquad n\in\mathbb Z.$$ Note that here, $\log$ is the usual function logarithm defined on the positive real half-line.
267k 27 27 gold badges 270 270 silver badges 531 531 bronze badgesA hint: The formula $$\cos x+\sin x=\sqrt\>\sin\left(x+<\pi\over4>\right)$$ known from high-school trigonometry also holds for complex $x$.

Yet another answer:
First, let's recognize why we need to go to complex variables. Recalling that $\cos\frac<\pi>=\sin\frac<\pi>=\frac>$, we have from the cosine addition formula
$$\sin z+\cos z = \sqrt\cdot\left[\sin\frac<\pi>\sin z+\cos\frac<\pi>\cos z\right]=\sqrt\cos\left(z-\frac<\pi>\right)$$ as several other answers have already noted. This has a maximum value of $\sqrt$ for real $z$, so we'll need complex $z$ if we want to get a value of $2$ instead.
Keeping in mind that the closest approach for real $z$ was $z=\pi/4$, we make the substitution $z=\frac<\pi>+i\tau$ with the anticipation that $\tau$ should 'mostly' be imaginary. Thus gives the equation $$\sqrt\cos\left(z-\frac<\pi>\right)=\sqrt\cos(i\tau)=\sqrt\cosh \tau=2$$ which immediately yields $\tau=\pm \cosh^ \sqrt$ as the principal solutions (recall that hyperbolic cosine is an even function). Thus $\boxed

В данной статье остановимся кратко на решении задач C1 из ЕГЭ по математике. Эти задания представляют собой уравнения, которые требуется, во-первых, решить (то есть найти их решения, причем все ), во-вторых, осуществить отбор решений по тому или иному ограничению. В последние годы на ЕГЭ по математике в заданиях C1 школьникам предлагаются для решения тригонометрические уравнения, поэтому в данной статье разобраны только они. Примеры структурированы по методам решения уравнений, от самых элементарных, до достаточно сложных.
Прежде чем перейти к разбору конкретных тригонометрических уравнений, вспомним основные формулы тригонометрии. Приведем их здесь в справочном виде.

Основные тригонометрические формулы

Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений
принадлежащие промежутку
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем (на всякий случай, эта запись означает, что числа и принадлежат множеству целых чисел):
Арккосинус есть число, заключенное в интервале от до , косинус которого равен .
Арксинус есть число, заключенное в интервале от до , косинус которого равен .
Другими словами, нам нужно подобрать такое число из промежутка косинус которого был бы равен Это число Используя это, получаем:
Вообще, значения тригонометрических функций от основных аргументов нужно знать. Их совсем чуть-чуть:
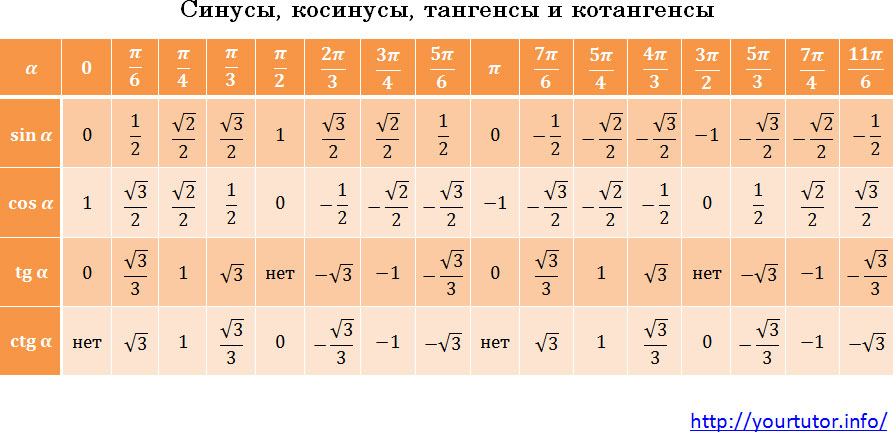
Таблица значений тригонометрических функций
Хотя на самом деле запоминать их вовсе не обязательно. Существует очень простой алгоритм, используя который, можно в уме легко вычислять значения тригонометрических функций всех основных аргументов. Просто у каждого он свой. Придумайте его и для себя. Просто посмотрите на эту таблицу. Числа в ней расположены не случайным образом, определенная закономерность есть, постарайтесь ее найти.
1)
2)
Задача для самостоятельного решения №1. Найдите корни уравнения принадлежащие промежутку
Решение линейных тригонометрических уравнений
принадлежащие промежутку
Решение. Подобные уравнения решаются один весьма интересным, на мой взгляд, способом. Разделим обе части на , уравнение тогда примет вид:
Подберем такое число, синус которого равен а косинус равен Например, пусть это будет число . С учетом этого перепишем уравнение в виде:
Присмотревшись, слева от знака равенства усматриваем разложение косинуса разности и Это и есть ключ к решению. Имеем:
Осуществляем отбор решений, входящих в промежуток :
Задача для самостоятельного решения №2. Найдите корни уравнения принадлежащие промежутку
Решение тригонометрических уравнений методом замены переменной
Пример 3. Дано уравнениеа) Решите уравнение.
б) Укажите корни, принадлежащие отрезке
Решение. Сразу оговорим ограничения, накладываемые на переменную в этом уравнении: Откуда взялось это ограничение? Правильно, функция не существует при этих значениях Используем замену переменной: Тогда уравнение принимает вид:
Переходим к обратной замене:
Осуществляем отбор решений. Проведем его на этот раз с использованием единичной окружности.

Отбор корней с помощью единичной окружности
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку
Решение тригонометрических уравнений методом разложения на множители
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку
Решение. Равносильными преобразования приводим уравнение к виду:
Осуществляем отбор решений с помощью единичной окружности.

Отбор решений с помощью единичной окружности
Из рисунка видно, что в интересующий нас промежуток входят только два значения из всех этих серий:
Задача для самостоятельного решения №4. Дано уравнение
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку
Комбинированные уравнения
Решение. Данное уравнение эквивалентно следующей системе:
Обратите внимание! Писать, что нет никакой необходимости, поскольку по условию это выражение равно выражению которое, в свою очередь, больше или равно нулю.
Решаем первое уравнение системы:
Ответ:
Решение. Данное уравение равносильно системе:
Тригонометрическая функция синус положительна в первой и второй координатной четвертях, поэтому из полученных серий выбираем только эту:
Раз уж мы с этим столкнулись, не лишним будет повторить, какие знаки принимают тригонометрические функций в различных координатных четвертях:
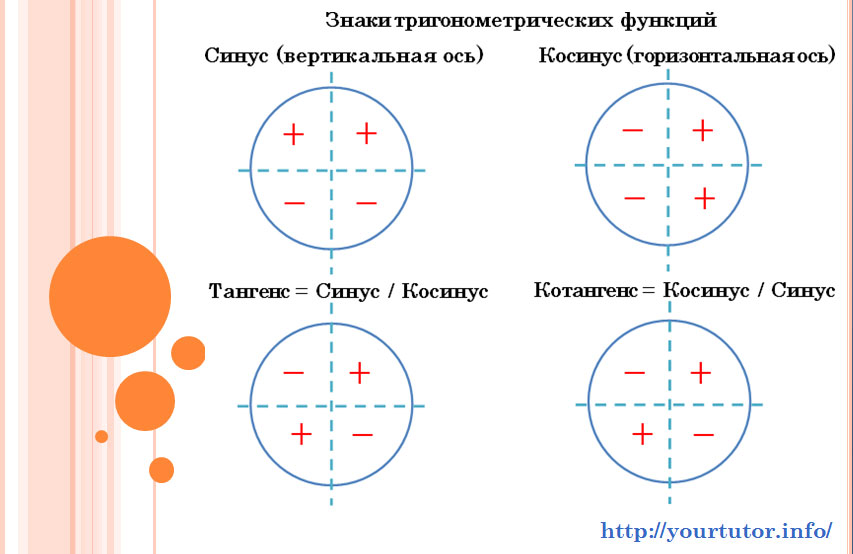
Знаки функций, входящих в тригонометрические уравнения, по координатным четвертям
Ответ:
Задача для самостоятельного решения №6. Решите уравнение:
Ответ:Решение. Область допустимых значения уравнения определяется условием: то есть Разобьем решение на два случая:
1) Пусть тогда уравнение принимает вид:
Последнее равенство неверно, поэтому в данном случае решений у уравнения не будет.
2) Пусть тогда уравнение принимает вид:
Условию удовлетворяет только последняя серия.
Ответ:
Задача для самостоятельного решения №7. Решите уравнение:
Ответ:ЕГЭ по математике 2012 позади, все в ожидании результатов, которые обещали объявить во вторник 19 июня. Сейчас уже поздно желать высоких баллов на экзаменах нынешним выпускникам. Но вот пожелать успехов сегодняшним десятиклассникам я возможности не упущу. Удачи вам в подготовке и помните, что чем раньше она начнется, тем лучше будут результаты на экзамене.

Читайте также:

