Машинариум крестики нолики исходный код
Обновлено: 02.07.2024
Эта публикация удалена, так как она нарушает рекомендации по поведению и контенту в Steam. Её можете видеть только вы. Если вы уверены, что публикацию удалили по ошибке, свяжитесь со службой поддержки Steam.
Этот предмет несовместим с Machinarium. Пожалуйста, прочитайте справочную статью, почему этот предмет может не работать в Machinarium.
Доступность: скрытый
Этот предмет виден только вам, администраторам и тем, кто будет отмечен как создатель.
Доступность: только для друзей
В результатах поиска этот предмет сможете видеть только вы, ваши друзья и администраторы.
Продолжая тему интеллектуальных систем, предлагаю написать алгоритм для игры в крестики-нолики по правилам , предложенным в Machinarium.
Описание «Идеальной» игры «Крестики-Нолики»
Для начала давайте опишем, что мы понимаем под «идеальной» игрой — если я играю идеально, я или побеждаю в игре, или играю вничью. В случае если я играю против другого «идеального» игрока, я всегда играю вничью.
Можно ли описать эти требования количественно? Давайте для всех возможных вариантов конечного состояния игры назначить какое-то количество очков:
- Я победил, ура! Я получаю 10 очков!
- Я проиграл, блин. Я теряю 10 очков (потому, что другой игрок получает 10 очков).
- Ничья. Я получаю ноль, и другой игрок получает ноль.
В заключение
От переводчика
Перевод сделан с разрешения автора. Мне понравилась эта статья тем, что она просто и наглядно описала алгоритм Минимакс. В статье присутствуют неточности и упрощения а также, местами, неточная терминология.
Игры с нулевой суммой
Прежде всего, следует отметить, что крестики-нолики - это игра с нулевой суммой. То есть игра, в которой выигрыш одного игрока означает проигрыш другого. К играм с нулевой суммой также можно отнести шашки, шахматы, го и многие другие игры, список которых вы легко продолжите сами. Ко многим таким играм применимы рассуждения изложенные в первой части статьи.Дерево игры (решений)
Начнем с малого, с классических крестиков-ноликов на поле 3 на 3. Процесс игры можно представить в виде графа, узлы которого представляют собой состояния игрового поля после хода одного из игроков: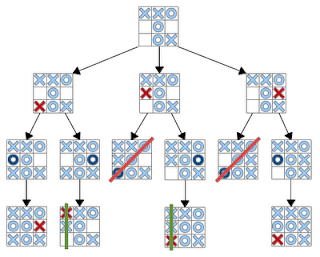 |
| Пример дерева игры в крестики-нолики |
Минимаксная процедура
Чтобы сократить дерево игры, можно поступать по аналогии с человеческим решением: человек тоже не способен продумать все варианты развития игры в соответствии со своим ходом, но он может продумать возможные варианты на несколько ходов вперед и выбрать наилучший из них. Количество шагов, на которое способен продумать игру человек, ограничено его интеллектуальными способностями. В случае с компьютерным решением, таким ограничением может стать память или время работы алгоритма. В простейшем случаем можно ограничиться глубиной раскрытия дерева. В таком случае, мы, конечно, рискуем выбрать ход, который будет привлекательным при выбранной глубине раскрытия дерева решений, но окажется проигрышным в более долгосрочной перспективе. Но не будем пессимистами! Самый интересный аспект такого подхода, это способ оценки выгоды от того или иного хода. В самом простейшем случае, можно выделить некоторые состояния игрового поля (ничья, победа и поражение) и присвоить каждому из них некоторый числовой коэффициент(оценку). |
| Пример оценок игрового поля (none = 0; draw = 2; win = 5; lose = -5) |
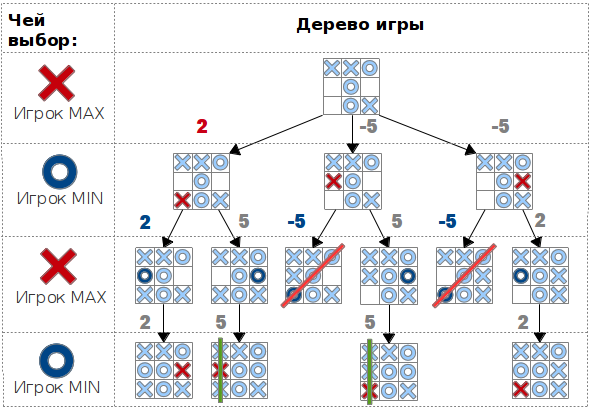 |
| Пример дерева игры, раскрытого на глубину в три хода |
Алгоритм
Для лучшего понимания алгоритма, привожу пример его реализации на вымышленном языке программирования:- Функция isTerminal проверяет, не достигнуто ли терминальное состояние на игровом поле. Терминальное состояние, это состояние при котором наступил выигрыш одного из игроков, или исчерпаны все возможные ходы, или выполнено условие прекращения раскрытия дерева игры (достигнута максимальная глубина / закончилась память).
- Функция heuristic дает эвристическую оценку состояния игрового поля.
- Функция children , при каждом обращении к ней, возвращает следующего потомка текущей оцениваемой позиции в дереве игры. Т.е. раскрывает дерево игры на следующую глубину.
Исходя из этого наблюдения, можно сократить код до одной функции:
При выборе одного из вариантов(MAXIMIN или MINIMAX) будьте внимательны, очень важно не напутать с аргументами при первом вызове этих функций. Если вершина раскрыта за игрока MAX (последний ход был игрока MAX), то следует вызывать функцию MINIMAX или -MAXIMIN.
Что же, с помощью минимаксной процедуры количество раскрываемых вершин существенно сократилось, но для реализации алгоритма, способного потягаться с сильным игроком, может понадобиться раскрывать дерево игры на достаточно большую глубину, а вместе с тем производить оценку все большего количества вершин. Это может приводить к существенным издержкам как по времени, так и по памяти. Поэтому, не смотря на то, что минимаксная процедура существенно сокращает количество раскрываемых вершин, она все еще не дает приемлемых результатов.
Если вернуться к приводимому ранее примеру дерева игры, то можно заметить следущее, после того, как был найден ход, приводящий крестиков как минимум к ничьей, этот ход становится меньшим из того, на что они согласны. Когда начнется рассмотрение второго хода(на глубине 1), и будет найдена проигрышная вершина, раскрывать следующую (на глубине 2) уже не будет смысла, так как для кружков худшее на что они согласны, это оценка -5, которая в свою очередь меньше чем самые худшие ожидания для крестиков. Стало быть, второй ход(вторая вершина на глубине 1) выбран не будет.
Осознать это наблюдение с первого раза довольно трудно, но тем не менее оно может помочь сократить количество раскрываемых вершин в дереве игры. На подобных рассуждениях строится следующий алгоритм, называемый альфа-бета отсечения.
Альфа-бета отсечения. Общие идеи
Давайте отвлечемся от крестиков-ноликов и рассмотрим дерево гипотетической игры Кружки-ромбики (граф раскрывается для кружков, те кружки выбирают ход с максимальной оценкой, а ромбики с минимальной):Чтобы сократить количество раскрываемых вершин, можно воспользоваться оценкой, полученной для предыдущей вершины на этой же глубине. Для MAX, эта оценка будет предельной максимальной оценкой, а для MIN предельной минимальной. Такие оценки принято называть альфа и бета границами.
Вот как это работает: раскрытие корневой вершины начинается с эмпирически подобранными параметрами альфа и бета. В простейшем случае им присваиваются максимально и минимально допустимые оценки. Далее, дерево раскрывается на максимальную глубину, которая может определяться фиксированным значением глубины, временем или памятью. Производится эвристическая оценка полученных листов. Оценки сравниваются на предмет попадания в диапазон альфа-бета. Если раскрытие происходит за игрока MAX и оценка оказывается больше беты, или раскрытие происходит за игрока MIN и оценка оказывается меньше альфа, то дальнейшее рассмотрение вершин становится не целесообразным.
| Пример бета отсечения |
На приведенном выше рисунке представлен случай с бета отсечением. После раскрытия всех листьев в левой ветке и получив оценку 7 для первой вершины на глубине два, мы переходим к раскрытию второй вершины. Получая оценку для каждой дочерней ее вершины, сравниваем ее с полученной ранее оценкой 7. Если оценка вновь раскрытой вершины окажется больше, то нет смысла раскрывать остальные вершины, тк очевидно что выбор будет сделан в ползу вершины с оценкой 7. Аналогичные рассуждения применимы для параметра альфа.
Алгоритм
или в одну функцию:
Подобное решение может показаться не очевидным. Для более подробного рассмотрения того, как к нему придти, читайте перевод статьи Д.Е.Кнута и Р.У.Мура например здесь.
Давайте рассмотрим короткий пример.
На картинке изображено состояние игрового поля, и мой черед ходить. Я играю за «Х». Моя цель, очевидно, максимизация количества очков, которые я получу.

Верхняя часть картинки показывает состояние игры, и, в зависимости от моего выбора, я могу попасть в одно из трех состояний из нижней части картинки. Очевидно, что состояние, в котором я побеждаю (снизу слева) является наилучший. Если я не сделаю этот ход, игрок «О» может легко победить, и я не хочу, чтоб он победил. Таким образом, выберу ход, который принесет мне наибольшее число очков.
Но что мы знаем о втором игроке? Мы можем предположить, что он тоже играет с целью победить в игре. Игрок «О» хочет выбрать ход, который приведет к наименьшему выигрышу для нас, он хочет минимизировать наш выигрыш. Давайте посмотрим на вещи с точки зрения игрока «О» начиная с двух других состояний игры из предыдущего примера, тех, в которых я не побеждаю:

Выбор очевиден, «О» выберит один из ходов, который приведет нас к результату -10.
Описание алгоритма Минимакс
Суть алгоритма Минимакс это поочередный перебор возможных ходов двух игроков, при котором мы считаем, что игрок «чья очередь» выберет ход, приносящий максимальное количество очков. Предположим, что мы играем за игрока «Х», тогда описание алгоритма будет примерное таким:
- Если игра закончена, вернуть количество очков для игрока «Х»
- В противном случае, получить список новых состояний игровой области для каждого возможного хода
- Оценить возможный выигрыш для каждого возможного состояния
- Для каждого из возможных состояний добавить «Минимакс» оценку текущего состояния
- Если ход игрока «Х» — вернуть ход с максимальным количеством очков
- Если ход игрока «О» — вернуть ход с минимальным количеством очков
- В состоянии 1 — очередь ходить у игрока «Х». «Х» генерирует состояния 2, 3 и 4 и рекурсивно применяет алгоритм к сгенерированным состояниям
- Состояние 2 добавляет выигрыш в размере +10 к оценке состояния 1, потому что игра выиграна
- Состояния 3 и 4 не являются конечными состояниями, поэтому из состояния 3 генерируются состояния 5 и 6, из состояния 4 генерируются состояния 7 и 8, после чего к каждому из сгенерированных состояний применяется алгоритм Минимакс.
- Состояние 5 добавляет «проигрыш в размере -10 для состояния 3, то же самое происходит и с состоянием 7 для состояния 4.
- Состояния 6 и 8 генерируют лишь конечные выигрышные состояния, поэтому каждое из них добавляет выигрыш в размере +10 для состояний 3 и 4.
- Так как на состояниях 3 и 4 очередь ходить игрока „О“, „О“ будет искать наименьший выигрыш. Исходя из выбора в -10 и +10, оба состояния вернут -10
- Наконец, оценка выигрыша для состояний 2, 3 и 4 будет рассчитана как +10, -10 и -10 соответственно. Так как игрок „Х“ стремиться максимизировать выигрыш, будет сделан выбор в пользу состояния 2.
Реализация алгоритма Минимакс
Надеюсь теперь у вас есть общее представление, как алгоритм Минимакс определяет наилучший ход. Давайте рассмотрим имплементацию алгоритма, чтоб закрепить наше понимание.
Вот функция, которая производит оценку состояния:
Достаточно просто, вернуть +10 если текущий игрок побеждает в игре, -10, если проигрывает и 0 в случае ничьи. Вы также можете отметить, что с точки зрения алгоритма нет разницы, какой это игрок (»Х" или «О»), важно лишь чей ход.
А теперь собственно сам алгоритм; обратите внимания что в приведенном варианте выбор хода это просто адрес ячейки на поле, т.е. [0,2] это правая верхняя ячейка на игровом поле размером 3x3.
Когда алгоритм выполняется в классе PerfectPlayer, выбор наилучшего ходя сохраняется в переменной choice, которая впоследствии используется для того, чтобы вернуть новое состояние игры в которое мы попадаем в результате выбранного игроком хода.
Даем противнику хороший бой: глубина
Наилучшим улучшением для алгоритма будет изменить его так, чтоб «идеальный игрок» играл «идеально» до самого конца, т.е. взять «глубину» (количество ходов до возможного проигрыша) в расчет при выборе хода. Простыми словами, идеальный игрок будет играть идеально, и постарается играть так долго, как только сможет.
Для того чтобы достигнуть такого результата мы будем отнимать глубину рекурсии\количество ходов от конечного состояния игры. Т.е. чем больше ходов до минимального выигрыша (и чем меньше ходов до максимального) — тем лучше.
Так, каждый раз при вызове алгоритма Минимакс глубина будет увеличена на 1, и когда мы наконец рассчитаем возможный выигрыш для конкретного конечного состояния игры мы введем поправку на глубину. Давайте посмотрим, как это выглядит на примере следующего дерева ходов:

Теперь учет глубины (как показано черным слева) приводит к тому, что оценка различается для каждого конечного состояния, и, потому что на первом уровне Минимакс будет пытаться максимизировать возможный выигрыш (т.к. ход игрока «О») предпочтительная оценка выигрыша составит -6, т.к. это выше чем альтернативный вариант в -8. И потому, несмотря на то, что игроку грозит верная смерть, наш надежный «идеальный игрок» выберет ход, который приведет к достойной смерти, и заблокирует выигрыш игрока «Х».
Интуитивный подход
Описанная в данной статье эвристика слишком проста, чтобы позволить достаточно сократить дерево игры и не потерять ощущения интеллектуальности компьютерного оппонента на заявленном в самом начале поле 10 на 10 клеток. Не станем останавливаться на достигнутом и попробуем зайти с другого края.
Отвлечемся от общепринятого подхода к решению игр с нулевой суммой и попытаемся проанализировать собственное мышление при игре в крестики нолики. Тут пора бы признаться, что мы редко смотрим на много шагов вперед, а просто стремимся действовать по следующим правилам: чем длиннее собирается комбинация в результате нашего хода, тем лучше, и чем большую комбинацию мы подпортим противнику, тем опять же нам лучше. Попытаемся обучить такой стратегии компьютер.
Введем функцию оценки каждого хода следующего вида:
где m - оцениваемый ход, G(m) - оценка пользы от хода для игрока, Q(m) - оценка степени вредительства противнику.
Мерой, для хода, может послужить длина собираемой комбинации k и длина нарушаемой комбинации противника k' в каждом из возможных четырех направлений (по вертикали, по горизонтали и в двух диагоналях):
 |
| Пример потенциальных областей для сбора выигрышной комбинации длинной 4 |

- для горизонтальной линии k = 1, k' = 1;
- для вертикальной линии k = 4, k' = 0;
- для первой диагонали (\) k = 0, k' = 4;
- для второй диагонали (/) k = 2, k' = 0.
Если функция G растет быстрее, чем Q, алгоритм ведет себя более агрессивно, стремясь как можно скорее закончить игру. Если быстрее растет функции Q, то алгоритм наоборот, проявляет осторожность и стремится чаще мешать противнику.
Как выбрать функции G и Q
При выборе функций G и Q трудно найти универсальную формулу, но можно опереться на ключевые ситуации в игре, и сделать выбор исходя из собственных предпочтений в них.
Прежде всего, чтобы алгоритм не упускал возможность завершить игру в свою пользу, необходимо выполнение следующего условия:
где W - длина выигрышной комбинации.
Так же, глупо отдавать предпочтение своему ходу, когда противник в шаге от победы:
 |
| Игра за крестики до 5 |
Коэффициент 4 обусловлен тем, что возможна(хотя и крайне мало вероятна) ситуация, когда оцениваемый ход будет получать значения k близкие к k' сразу в четырех направлениях.
И еще один пример, который иллюстрирует ситуацию, когда может быть сделан нежелательный, на мой взгляд, выбор:

Выбранные функции удовлетворяют условиям (2) и (3) уже при значении k и k' равным 3, и на практике дают вполне приемлемые результаты.
Что еще можно сделать
Ко всему уже изложенному, у меня остались еще несколько соображений, на счет улучшения качества алгоритма, которыми мне бы хотелось поделиться.Игнорировать ходы, которые в принципе не могут привести к победе
Идея в том, что нет смысла производить оценку хода в некоторой линии, если количество свободных и собственных ячеек в этой линии, около ячейки, хода меньше выигрышной длины.Объединить интуитивные рассуждения с минимаксной процедурой.
Не смотря на то, что интуитивный подход сам по себе дает не плохие результаты, его можно применить в качестве эвристики в минимаксной процедуре. Это должно повысить качество решений, принимаемых алгоритмом.Упростить определение терминального состояния.
Условием терминального состояния, для минимаксной процедуры, является победа одного из игроков или ничья. Если для представления игрового поля вы используете двумерный массив, то можно избежать его перепросмотра с целью найти победную комбинацию после каждого совершенного хода.
Идея заключается в том, что состояние игры изменяется в результате хода, который влияет не на все поле целиком, а только на окрестность ячейки, в которую был выполнен ход, в радиусе выигрышной длины. Достаточно проверять, не привел ли ход к завершению игры и в соответствии с этим менять состояние игрового поля.
Для ничьи, ничего умнее полного перебора предложить не могу. Были мысли по кешированию свободных клеток, но это скорее только навредит.
Сократить количество потенциальных ходов
Обычно, в качестве возможных ходов, выбираются пустые клетки поля. Но если поле имеет относительно большой размер, вариантов ходов может оказаться очень много. Есть подозрения, что достаточно рассматривать не все пустые клетки поля, а только пустые клетки в окрестности уже занятых:

Такой подход дает большой выигрыш на больших полях, практически нивелируя влияние размера поля на время действия алгоритма.
Добавить критерии оценки хода
Помимо длины, собираемой в результате хода последовательности, в роли критерия качества хода можно брать полное количество своих (или чужих) клеток в ряду:
Недавно я написал непобедимую игру «Крестики-Нолики». Это был интересный и поучительный проект, который многому меня научил. Если у вас есть желание посмотреть результат — это можно сделать здесь.

Для того чтобы сделать игру непобедимой, было необходимо создать алгоритм, который может рассчитать все возможные ходы для «компьютерного» игрока. Далее, нужно использовать некоторую метрику, чтобы определить, какой ход является предпочтительным. После долгих исследований стало понятно, что алгоритм Минимакс, был тем, что мне нужно.
Понимание основ алгоритма и реализация игры заняли некоторое время. Я нашел много примеров кода и объяснений, тем не менее это оказалось не такой уж простой затеей. Надеюсь этот пост поможет некоторым из читателей оценить элегантность этого алгоритма.
Идеальный игрок-самоубийца
Эта имплементация алгоритма позволит вам создать игру в «крестики-нолики», в которую вы не сможете победить. Но есть маленький нюанс, который я обнаружил в процессе тестирования игры. В случае, если мой «идеальный игрок» обнаружит состояние, в котором он или проиграет, или закончит вничью, его ход будет самоубийственным. Проще говоря, алгоритм говорит «я все равно проиграю, поэтому без разницы сейчас, или через 6 ходов».
Я обнаружил это когда передал явно некорректное состояние игрового поля и попытался выяснить, какой ход предложит алгоритм. Я ожидал, что «идеальный игрок» попытается помешать мне выиграть так долго, как сможет, но этого не произошло:

Давайте рассмотрим, что происходит здесь через призму возможных ходов (для простоты я удалил некоторые состояния)

- В случае если игровое поле в состоянии 1, и оба игрока играют идеально, и компьютер играет на стороне «О», «О» принимает решение идти в состояние 5, что ведет к немедленному проигрышу, когда игрок «Х» переходит в состояние 9.
- Но если «О» заблокирует ход «Х» перейдя в состояние 3, «Х» заблокирует потенциально победный ход «О», как показано в состоянии 7.
- Исходя из этого очевидно, что «Х» победит, как показано в состояниях 10 и 11, несмотря на то, какой ход выберет «О».
Черт побери, что же мастер «крестиков-ноликов» должен сделать?
Читайте также:

